题目内容
如果函数f(x)=ax2-3x+4在区间(-∞,6)上单调递减,则实数a的取值范围是______.
[0, ]
]
 ]
](1)当a=0时,f(x)=-3x+4,函数在定义域R上单调递减,故在区间(-∞,6)上单调递减.(2)当a≠0时,二次函数f(x)图象的对称轴为直线x= .因为f(x)在区间(-∞,6)上单调递减,所以a>0,且
.因为f(x)在区间(-∞,6)上单调递减,所以a>0,且 ≥6,解得0<a≤
≥6,解得0<a≤ .综上所述,0≤a≤
.综上所述,0≤a≤ .
.
 .因为f(x)在区间(-∞,6)上单调递减,所以a>0,且
.因为f(x)在区间(-∞,6)上单调递减,所以a>0,且 ≥6,解得0<a≤
≥6,解得0<a≤ .综上所述,0≤a≤
.综上所述,0≤a≤ .
.
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
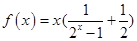
 在定义域内恒成立;
在定义域内恒成立; 时,
时,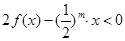 恒成立,求m的取值范围.
恒成立,求m的取值范围.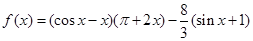 ,
,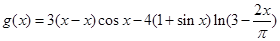 .
.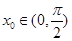 ,使
,使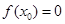 ;
;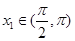 ,使
,使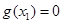 ,且对(1)中的
,且对(1)中的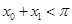 .
.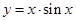 ;②
;② ;③
;③ ;④
;④ 的部分图象如下:
的部分图象如下: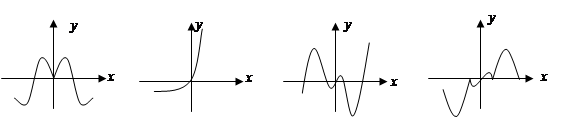
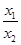 )=f(x1)-f(x2),且当x>1时,f(x)<0.
)=f(x1)-f(x2),且当x>1时,f(x)<0.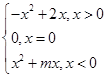 是奇函数.
是奇函数.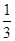 )x-1,则f(
)x-1,则f(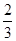 ),f(
),f(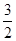 ),f(
),f(