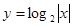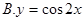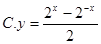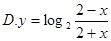题目内容
已知函数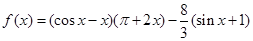 ,
,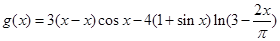 .
.
证明:(1)存在唯一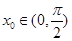 ,使
,使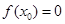 ;
;
(2)存在唯一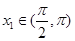 ,使
,使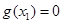 ,且对(1)中的
,且对(1)中的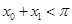 .
.
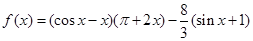 ,
,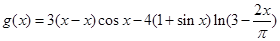 .
.证明:(1)存在唯一
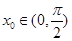 ,使
,使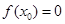 ;
;(2)存在唯一
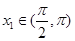 ,使
,使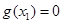 ,且对(1)中的
,且对(1)中的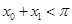 .
.(1)详见解析;(2) 详见解析.
试题分析:(1)当
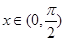 时,
时,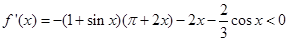 ,函数
,函数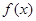 在
在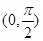 上为减函数,又
上为减函数,又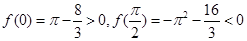 ,所以存在唯一
,所以存在唯一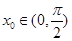 ,使
,使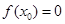 .(2)考虑函数
.(2)考虑函数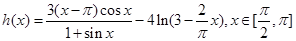 ,令
,令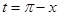 ,则
,则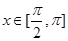 时,
时,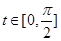 ,
,记
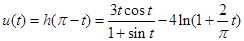 ,则
,则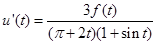 ,有(1)得,当
,有(1)得,当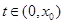 时,
时,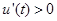 ,当
,当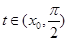 时,
时,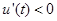 .在
.在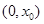 上
上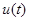 是增函数,又
是增函数,又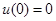 ,从而当
,从而当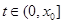 时,
时,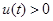 ,所以
,所以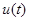 在
在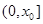 上无零点.在
上无零点.在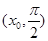 上
上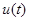 是减函数,又
是减函数,又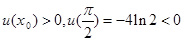 ,存在唯一的
,存在唯一的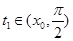 ,使
,使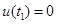 .所以存在唯一的
.所以存在唯一的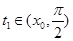 使
使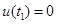 .因此存在唯一的
.因此存在唯一的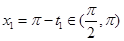 ,使
,使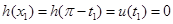 .因为当
.因为当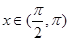 时,
时,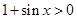 ,故
,故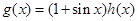 与
与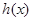 有相同的零点,所以存在唯一的
有相同的零点,所以存在唯一的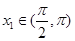 ,使
,使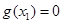 .因
.因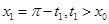 ,所以
,所以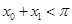 ,即命题得证.
,即命题得证.(1)当
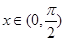 时,
时,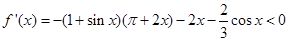 ,函数
,函数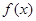 在
在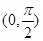 上为减函数,又
上为减函数,又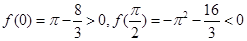 ,所以存在唯一
,所以存在唯一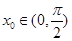 ,使
,使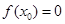 .
.(2)考虑函数
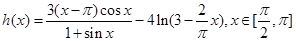 ,
,令
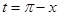 ,则
,则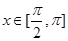 时,
时,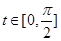 ,
,记
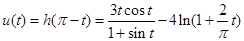 ,则
,则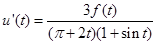 ,
,有(1)得,当
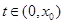 时,
时,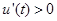 ,当
,当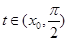 时,
时,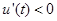 .
.在
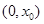 上
上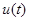 是增函数,又
是增函数,又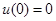 ,从而当
,从而当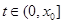 时,
时,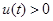 ,所以
,所以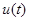 在
在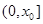 上无零点.
上无零点.在
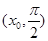 上
上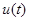 是减函数,又
是减函数,又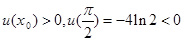 ,存在唯一的
,存在唯一的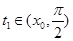 ,使
,使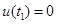 .
.所以存在唯一的
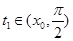 使
使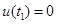 .
.因此存在唯一的
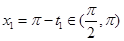 ,使
,使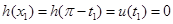 .
.因为当
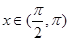 时,
时,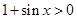 ,故
,故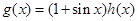 与
与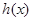 有相同的零点,所以存在唯一的
有相同的零点,所以存在唯一的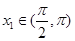 ,使
,使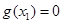 .
.因
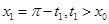 ,所以
,所以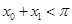

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
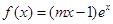 在
在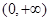 上单调递增,则实数
上单调递增,则实数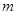 的取值范围是 .
的取值范围是 .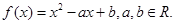
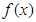 在区间
在区间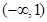 上单调递减,则
上单调递减,则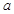 的取值范围 .
的取值范围 .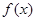 在R上存在导数
在R上存在导数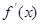 ,对任意的
,对任意的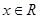 有
有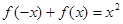 ,且在
,且在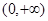 上
上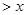 .若
.若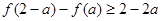 ,则实数
,则实数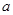 的取值范围 .
的取值范围 .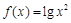 的单调递减区间是________.
的单调递减区间是________.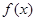 是定义在
是定义在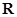 上的偶函数,且
上的偶函数,且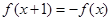 ,若
,若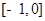 上单调递减,则
上单调递减,则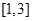 上是( )
上是( )