题目内容
已知函数f(x)=x3+3x对任意的m∈[-2,2],f(mx-2)+f(x)<0恒成立,则x的取值范围为________.
(-2,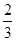 )
)
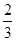 )
)∵函数f(x)=x3+3x是奇函数,且在定义域f(x)=x3+3x上单调递增,∴由f(mx-2)+f(x)<0得f(mx-2)<-f(x)=f(-x),即mx-2<-x,令g(m)=xm+(x-2),由题意知g(2)<0,g(-2)<0,令g(m)=xm+(x-2),g(2)<0,g(-2)<0,
∴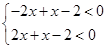 ,解得-2<x<
,解得-2<x<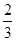 .
.
∴
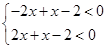 ,解得-2<x<
,解得-2<x<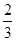 .
.
练习册系列答案
相关题目
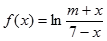 在其定义域上为奇函数.
在其定义域上为奇函数.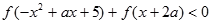 对任意实数
对任意实数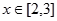 恒成立,求实数
恒成立,求实数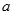 的取值范围.
的取值范围.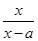 (x≠a).
(x≠a).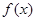 在R上存在导数
在R上存在导数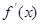 ,对任意的
,对任意的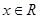 有
有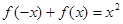 ,且在
,且在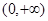 上
上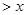 .若
.若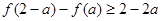 ,则实数
,则实数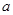 的取值范围 .
的取值范围 .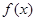 是定义在
是定义在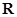 上的偶函数,且
上的偶函数,且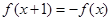 ,若
,若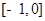 上单调递减,则
上单调递减,则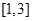 上是( )
上是( )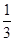 )=0,则不等式f(
)=0,则不等式f(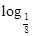 x)>0的解集是( )
x)>0的解集是( )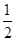 )
) ≤x≤9.
≤x≤9.