题目内容
已知函数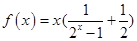
(1)判定并证明函数的奇偶性;
(2)试证明 在定义域内恒成立;
在定义域内恒成立;
(3)当 时,
时,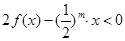 恒成立,求m的取值范围.
恒成立,求m的取值范围.
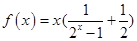
(1)判定并证明函数的奇偶性;
(2)试证明
 在定义域内恒成立;
在定义域内恒成立;(3)当
 时,
时,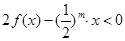 恒成立,求m的取值范围.
恒成立,求m的取值范围.(1)偶函数,(2)详见解析,(3)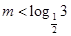 .
.
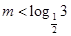 .
.试题分析:(1)判定函数的奇偶性,首先判定定义域是否关于原点对称,定义域为:
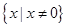 关于原点对称,其次研究
关于原点对称,其次研究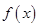 与
与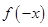 的相等或相反的关系:
的相等或相反的关系: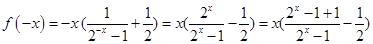
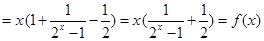 所以
所以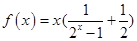 为偶函数,(2)由于函数
为偶函数,(2)由于函数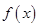 为偶函数,所以只需证明
为偶函数,所以只需证明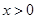 时
时 ,当
,当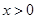 时,
时,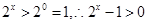
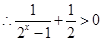 ,
,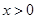 ,
,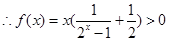 恒成立,当
恒成立,当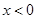 时,所以
时,所以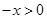 ,由(1)可知:
,由(1)可知: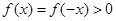 ,综上所述,
,综上所述, 在定义域内恒成立(3)恒成立问题一般利用变量分离法转化为最值问题.
在定义域内恒成立(3)恒成立问题一般利用变量分离法转化为最值问题. 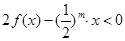 恒成立对
恒成立对 恒成立,∴
恒成立,∴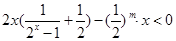 ,∴
,∴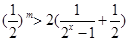 ,令
,令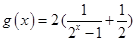 可证
可证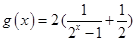 在[1,3]上为减函数 ∴
在[1,3]上为减函数 ∴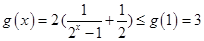 对
对 恒成立 ∴
恒成立 ∴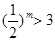 ,所以m的取值范围是
,所以m的取值范围是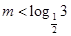 .
.试题解析:解:(1)
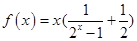 为偶函数,证明如下:
为偶函数,证明如下: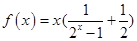 定义域为:
定义域为: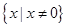 关于原点对称,
关于原点对称,对于任意
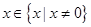 有: 2分
有: 2分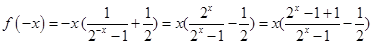
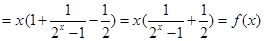 成立
成立所以
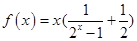 为偶函数 5分
为偶函数 5分(2)因为
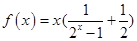 定义域为:
定义域为: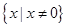 ,
,当
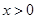 时,
时,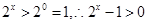
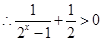 ,
,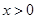 ,
,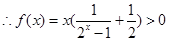 恒成立, 7分
恒成立, 7分当
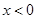 时,所以
时,所以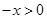 ,由(1)可知:
,由(1)可知: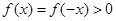 9分
9分综上所述,
 在定义域内恒成立 10分
在定义域内恒成立 10分(3)
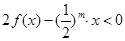 恒成立对
恒成立对 恒成立,
恒成立,∴
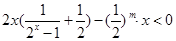 ,∴
,∴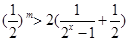 ,令
,令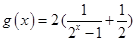
证明
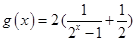 在[1,3]上为减函数(略)(不证明单调性扣2分)
在[1,3]上为减函数(略)(不证明单调性扣2分) ∴
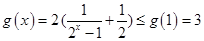 对
对 恒成立 12分
恒成立 12分∴
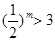
所以m的取值范围是
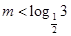 14分
14分
练习册系列答案
相关题目
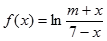 在其定义域上为奇函数.
在其定义域上为奇函数.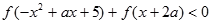 对任意实数
对任意实数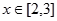 恒成立,求实数
恒成立,求实数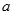 的取值范围.
的取值范围.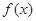 是
是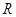 上的增函数,
上的增函数,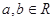 ,且
,且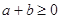 ,求证
,求证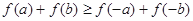
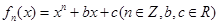 .
.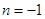 ,函数
,函数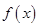 在区间
在区间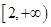 上是单调递增函数,求实数
上是单调递增函数,求实数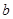 的取值范围;
的取值范围;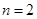 ,若对任意
,若对任意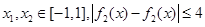 恒成立,求
恒成立,求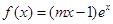 在
在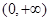 上单调递增,则实数
上单调递增,则实数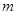 的取值范围是 .
的取值范围是 .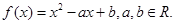
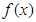 在区间
在区间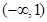 上单调递减,则
上单调递减,则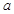 的取值范围 .
的取值范围 .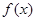 在R上存在导数
在R上存在导数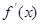 ,对任意的
,对任意的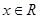 有
有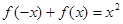 ,且在
,且在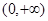 上
上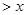 .若
.若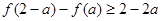 ,则实数
,则实数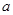 的取值范围 .
的取值范围 .