题目内容
9．计算：${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx=$\sqrt{3}$+$\frac{2π}{3}$．分析 ${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx表示如图阴影部分的面积，而S阴影=2S△ABC+S扇形CAD，解得即可．
解答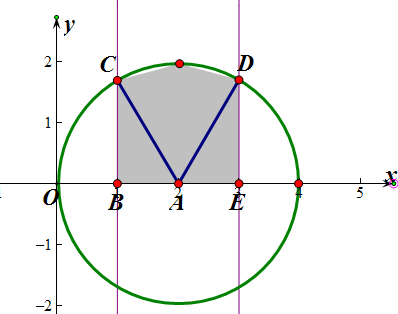 
解：令$\sqrt{4-（x-2）^{2}}$=y，y≥0，
∴（x-2）2+y2=4，
则${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx表示如图阴影部分的面积，
∴S阴影=2S△ABC+S扇形CAD=2×$\frac{1}{2}$×1×$\sqrt{3}$+$\frac{1}{6}$π×4=$\sqrt{3}$+$\frac{2π}{3}$，
∴${∫}_{1}^{3}$$\sqrt{4-（x-2）^{2}}$dx=$\sqrt{3}$+$\frac{2π}{3}$，
故答案为：$\sqrt{3}$+$\frac{2π}{3}$
点评 本题主要考查积分的几何意义，熟练掌握微积分基本定理是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
20．若a，b，c∈（0，+∞），且a+b+c=1，则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{\root{3}{2}}{3}$ | C． | $\frac{9}{2}$ | D． | $\frac{1}{9}$ |
17．$cos（\frac{19π}{3}）$的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
14．已知△ABC的三边满足（a+b+c）（a+b-c）=（$\sqrt{3}$+2）ab，则角C等于（ ）
| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
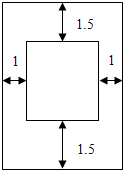某出版社出版一读物，为了排版设计的需要，规定：一页上所印文字的矩形区域需要占去150cm2，上、下边各要留1.5cm宽的空白，左、右两边各要留1cm宽的空白，出版商为了节约纸张，应选用怎样尺寸的矩形纸张来设计版面？