题目内容
3.若曲线C在顶点为O的角α的内部,A、B分别是曲线C上相异的任意两点,且α≥∠AOB,我们把满足条件的最小角α叫做曲线C相对点O的“确界角”.已知O为坐标原点,曲线C的方程为y=$\left\{\begin{array}{l}{\sqrt{1+{x}^{2}},x≥0}\\{2-\sqrt{1-{x}^{2}},x<0}\end{array}\right.$,那么它相对点O的“确界角”等于( )| A. | $\frac{π}{3}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
分析 画出函数f(x)的图象,过点O作出两条直线与曲线相切;再由两直线的夹角公式即可得到所求的“确界角”.
解答 解:画出函数f(x)的图象,过点O作出两条直线与曲线相切或曲线的渐近线,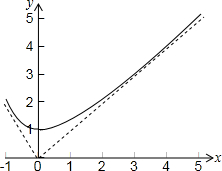
设它们的方程分别为y=k1x,y=k2x,
当x≥0时,y′=f′(x)=$\frac{x}{\sqrt{1+{x}^{2}}}$,
∵$\lim_{n→+∞}\frac{x}{\sqrt{1+{x}^{2}}}$=1,
∴渐近线y=k1x的倾斜角为$\frac{π}{4}$,
当x<0时,函数的导数f′(x)=$\frac{x}{\sqrt{1-{x}^{2}}}$,
设切点为(n,2-$\sqrt{1-{n}^{2}}$),
则对应的切线方程为y-(2-$\sqrt{1-{n}^{2}}$)=$\frac{n}{\sqrt{1-{n}^{2}}}$(x-n),
令x=0,y=0,则-(2-$\sqrt{1-{n}^{2}}$)=$\frac{-{n}^{2}}{\sqrt{1-{n}^{2}}}$,
解得n=-$\frac{\sqrt{3}}{2}$,则y=k2x的斜率k2=f′(-$\frac{\sqrt{3}}{2}$)=-$\sqrt{3}$,
则切线y=k2x的倾斜角$\frac{2π}{3}$,
由两直线的夹角θ=$\frac{2π}{3}$-$\frac{π}{4}$=$\frac{5π}{12}$,
故选:B
点评 本题考查新定义“确界角”及应用,考查导数的应用:求切线,利用导数的几何意义是解决本题的关键.

练习册系列答案
相关题目
1.设z1、z2∈C,则“z1、z2均为实数”是“z1-z2是实数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
8.设z1,z2∈C,则“z1、z2中至少有一个数是虚数”是“z1-z2是虚数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |