题目内容
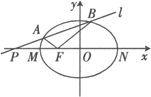
【题目】已知抛物线![]() 与直线
与直线![]() 相交于A、B两点.
相交于A、B两点.
(1)求证:![]() ;
;
(2)当![]() 的面积等于
的面积等于![]() 时,求k的值.
时,求k的值.
【答案】解: (1) 当k = 0时直线与抛物线仅一个交点, 不合题意, ………… 2分
∴k 0由y =" k" (x+1)得x =![]() –1 代入y 2=" –" x 整理得: y 2+
–1 代入y 2=" –" x 整理得: y 2+![]() y – 1 =" 0" , 2分
y – 1 =" 0" , 2分
设A (x 1, y 1), B (x 2, y 2) 则y 1+ y 2= –![]() , y 1y 2=" –1." ………… 2分
, y 1y 2=" –1." ………… 2分
∵A、B在y 2=" –" x上, ∴A (–![]() , y 1), B (–
, y 1), B (–![]() , y 2) ,
, y 2) ,
∴ kOA·kOB=![]() =
=![]() =" –" 1 .
=" –" 1 .
∴ OA^OB. …………… 3 分
(2) 设直线与x轴交于E, 则 E ( – 1 , 0 ) ∴|OE| =" 1" ,
【解析】
试题(1)可假设![]() ,分别代入抛物线方程与直线方程,化简整理可得
,分别代入抛物线方程与直线方程,化简整理可得![]() ,
,![]() ,利用向量垂直有
,利用向量垂直有![]() ,即证明
,即证明![]() ;(2)直线
;(2)直线![]() 与
与![]() 轴的交点为
轴的交点为![]() 的坐标为
的坐标为![]() ,则可将三角形
,则可将三角形![]() 拆为两个三角形
拆为两个三角形![]() ,两三角形具有相同的底边
,两三角形具有相同的底边![]() ,高分别为
,高分别为![]() 的纵坐标,利用(1)中
的纵坐标,利用(1)中![]() 的关系便可求得
的关系便可求得![]() 的面积函数,根据函数值求
的面积函数,根据函数值求![]() 的值.
的值.
试题解析:(1)证明:联立![]() ,消去x,得ky2+y-k=0.设A(x1,y1),B(x2,y2),则y1+y2=-
,消去x,得ky2+y-k=0.设A(x1,y1),B(x2,y2),则y1+y2=-![]() ,y1·y2=-1.因为y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即
,y1·y2=-1.因为y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即![]() =0,所以OA⊥OB.
=0,所以OA⊥OB.
(2)设直线l与x轴的交点为N,则N的坐标为(-1,0),
所以S△AOB=![]() |ON|·|y1-y2|
|ON|·|y1-y2|
=![]() ×|ON|×
×|ON|×![]()
=![]() ×1×
×1×![]() =
=![]() ,
,
解得k2=![]() ,所以k=±
,所以k=±![]() .
.

练习册系列答案
相关题目