题目内容
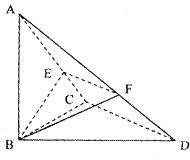
【题目】如图，在
中，
，
，
为线段
的垂直平分线，与交与点
为上异于
的任意一点.
求
的值；
判断
的值是否为一个常数，并说明理由．
【答案】
14；
是.
【解析】
法一：由题意及图形，可把向量
用两个向量
的表示出来，再利用数量积的公式求出数量积；
将向量
用与
表示出来，再由向量的数量积公式求数量积，根据其值的情况确定是否是一个常数；
法二：由题意可以以BC所在直线为x轴，DE所在直线为y轴建立坐标系，得出各点的坐标，由向量坐标的定义式求出
的坐标表示，由向量的数量积公式求数量积；
设E点坐标为
，表示出向量的坐标再由向量的数量积坐标表示公式求数量积即可.
法1：由已知可得
，
，
,
的值为一个常数
为线段BC的垂直平分线，L与BC交与点D，E为L上异于D的任意一点，
，
故：
解法2：以D点为原点，BC所在直线为x轴，L所在直线为 y轴建立直角坐标系，可求
，
此时
，
，
设E点坐标为，
，
常数
．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
