题目内容
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.


(1)写出图(1)表示的市场售价与时间的函数关系式![]() 写出图(2)表示的种植成本与时间的函数关系式
写出图(2)表示的种植成本与时间的函数关系式![]()
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
【答案】(1) ![]() ;
;![]() ;(2) 从2月1日开始的第50天时,上市的西红柿纯收益最大。
;(2) 从2月1日开始的第50天时,上市的西红柿纯收益最大。
【解析】
(1)根据图像写出解析式即可;
(2)得到![]()
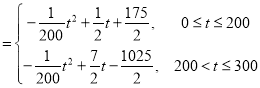 后,分两段求得各段的最大值,再比较大小可得分段函数的最大值.
后,分两段求得各段的最大值,再比较大小可得分段函数的最大值.
解:(1)由图(1)可得市场售价与时间的函数关系为![]()
由图(2)可得种植成本与时间的函数关系为![]()
(2)设![]() 时刻的纯收益为
时刻的纯收益为![]() ,则由题意得
,则由题意得![]()
即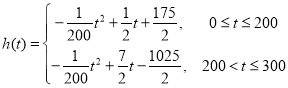
当![]() 时,配方得到
时,配方得到![]()
所以,当![]() 时,
时,![]() 取得区间
取得区间![]() 上的最大值为100;
上的最大值为100;
当![]() 时,配方整理得到:
时,配方整理得到:![]()
所以,当![]() 时,
时,![]() 取得区间
取得区间![]() 上的最大值为
上的最大值为![]() 。
。
综上,![]() 在区间
在区间![]() 上的最大值为100,此时
上的最大值为100,此时![]()
即从2月1日开始的第50天时,上市的西红柿纯收益最大。

 阅读快车系列答案
阅读快车系列答案【题目】根据以往的经验,某工程施工期间的将数量X(单位:mm)对工期的影响如下表:
降水量X | X<300 | 300≤X<700 | 700≤X<900 | X≥900 |
工期延误天数Y | 0 | 2 | 6 | 10 |
历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
【题目】某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元部分享受一定的折扣优惠,并按下表折扣分别累计计算:
可以享受折扣优惠金额 | 折扣率 |
不超过500元的部分 |
|
超过500元的部分 |
|
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所付金额为![]()
![]()
A.1500元B.1550元C.1750元D.1800元

