题目内容
在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离是( )
A.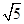 | B. | C.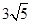 | D.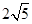 |
B
试题分析:如图:取BC的中点为E,连结AE及PE,由AB=AC=5知:
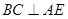 ,又因为PA⊥平面ABC,所以
,又因为PA⊥平面ABC,所以 ,从而有
,从而有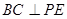 ,所以线段PE的长就是P到BC的距离;在
,所以线段PE的长就是P到BC的距离;在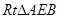 中有AE=4,又PA=8,在
中有AE=4,又PA=8,在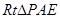 中有
中有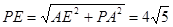 ,故选B.
,故选B.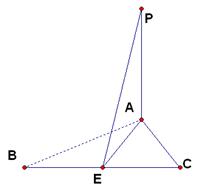

练习册系列答案
相关题目
题目内容
A.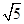 | B. | C.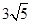 | D.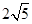 |
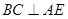 ,又因为PA⊥平面ABC,所以
,又因为PA⊥平面ABC,所以 ,从而有
,从而有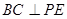 ,所以线段PE的长就是P到BC的距离;在
,所以线段PE的长就是P到BC的距离;在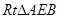 中有AE=4,又PA=8,在
中有AE=4,又PA=8,在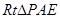 中有
中有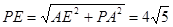 ,故选B.
,故选B.
