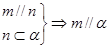题目内容
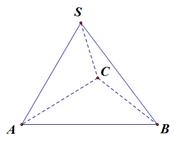
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.
二面角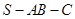 的余弦值为
的余弦值为 .
.
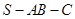 的余弦值为
的余弦值为 .
.试题分析:先作出二面角的平面角,由面面垂直可得线面垂直,可考虑利用三垂线定理作出二面角的平面角:故可先由题意
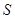 作
作 于
于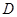 ,过
,过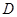 作
作 于
于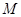 ,连
,连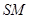 ,从而可得
,从而可得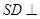 平面
平面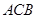 ,又由
,又由 ,故
,故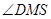 为二面角
为二面角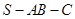 的平面角,从而问题就转化为求线段
的平面角,从而问题就转化为求线段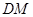 与
与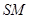 的长度,根据题意易得
的长度,根据题意易得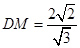 ,
, ,从而
,从而 ,即二面角
,即二面角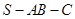 的余弦值为
的余弦值为 .
.试题解析:如图,过
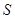 作
作 于
于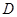 ,过
,过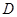 作
作 于
于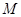 ,连
,连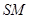 ,
,∵平面
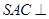 平面
平面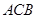 ,∴
,∴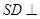 平面
平面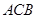 ,∴
,∴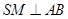 ,
,又∵
 ,∴
,∴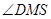 为二面角
为二面角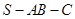 的平面角,在
的平面角,在 中,
中,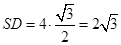 ,
,在
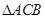 中过
中过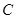 作
作 于
于 ,
,∵
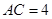 ,
,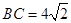 ,
,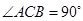 ,∴
,∴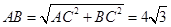 ,
,∵
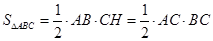 ,∴
,∴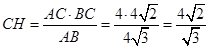 ,
,∵
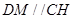 且
且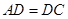 ,∴
,∴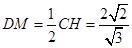 ,
,∵
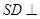 平面
平面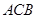 ,
, 平面
平面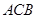 ,∴
,∴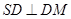 ,
,在
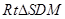 中,
中,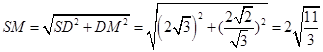 ,
,∴
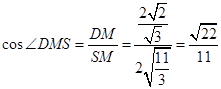 ,即二面角
,即二面角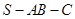 的余弦值为
的余弦值为 .
.

练习册系列答案
相关题目

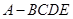 中,平面
中,平面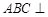 平面
平面 ;
;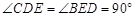 ,
, ,
,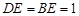 ,
,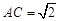 .
.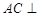 平面
平面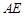 与平面
与平面 所成的角的正切值.
所成的角的正切值.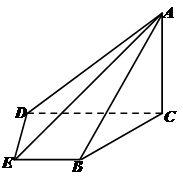
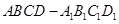 中,
中,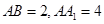 .
. 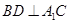 ;
;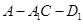 的余弦值;
的余弦值;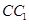 上是否存在点
上是否存在点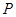 ,使得平面
,使得平面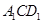
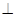 平面
平面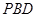 ,若存在,求出
,若存在,求出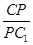 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.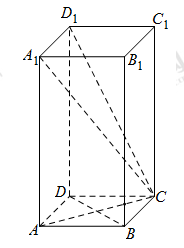
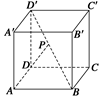
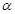 、
、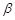 、
、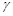 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ).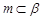 ,
,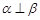 ,则
,则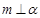
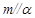 ,
,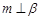 ,则
,则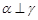 ,则
,则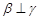
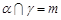 ,
,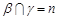 ,
,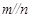 ,则
,则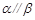
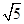

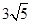
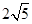
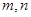 是不同的直线,
是不同的直线,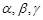 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: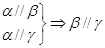 ②
②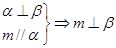
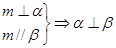 ④
④