题目内容
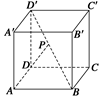
如图所示,正四面体V—ABC的高VD的中点为O,VC的中点为M.
(1)求证:AO、BO、CO两两垂直;
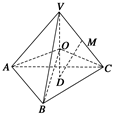
(2)求〈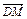 ,
,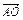 〉.
〉.
(1)求证:AO、BO、CO两两垂直;

(2)求〈
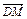 ,
,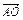 〉.
〉.(1)证明略(2)45°
(1) 设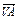 =a,
=a,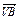 =b,
=b, 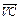 =c,正四面体的棱长为1,
=c,正四面体的棱长为1,
则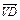 =
=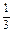 (a+b+c),
(a+b+c),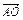 =
=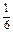 (b+c-5a),
(b+c-5a),
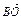 =
=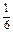 (a+c-5b),
(a+c-5b), 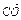 =
=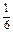 (a+b-5c)
(a+b-5c)
∴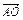 ·
·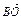 =
=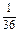 (b+c-5a)·(a+c-5b)
(b+c-5a)·(a+c-5b)
=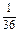 (18a·b-9|a|2)
(18a·b-9|a|2)
=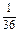 (18×1×1·cos60°-9)=0.
(18×1×1·cos60°-9)=0.
∴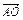 ⊥
⊥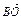 ,∴AO⊥BO,
,∴AO⊥BO,
同理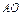 ⊥
⊥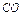 ,BO⊥CO,
,BO⊥CO,
∴AO、BO、CO两两垂直.
(2)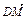 =
=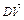 +
+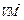 =-
=-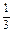 (a+b+c)+
(a+b+c)+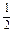
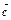
=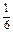 (-2a-2b+c).
(-2a-2b+c).
∴|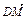 |=
|=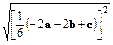 =
=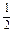 ,
,
|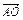 |=
|=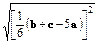 =
=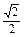 ,
,
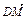 ·
·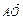 =
=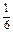 (-2a-2b+c)·
(-2a-2b+c)·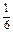 (b+c-5a)=
(b+c-5a)=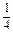 ,
,
∴cos〈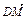 ,
,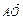 〉=
〉=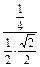 =
=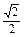 ,
,
∵〈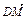 ,
,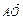 〉∈(0,
〉∈(0,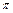 ),∴〈
),∴〈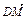 ,
, 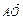 〉=45°.
〉=45°.
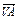 =a,
=a,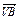 =b,
=b, 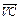 =c,正四面体的棱长为1,
=c,正四面体的棱长为1,则
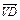 =
=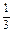 (a+b+c),
(a+b+c),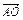 =
=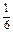 (b+c-5a),
(b+c-5a),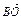 =
=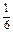 (a+c-5b),
(a+c-5b), 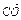 =
=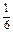 (a+b-5c)
(a+b-5c)∴
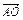 ·
·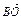 =
=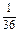 (b+c-5a)·(a+c-5b)
(b+c-5a)·(a+c-5b)=
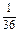 (18a·b-9|a|2)
(18a·b-9|a|2)=
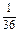 (18×1×1·cos60°-9)=0.
(18×1×1·cos60°-9)=0.∴
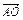 ⊥
⊥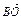 ,∴AO⊥BO,
,∴AO⊥BO,同理
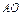 ⊥
⊥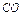 ,BO⊥CO,
,BO⊥CO,∴AO、BO、CO两两垂直.
(2)
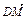 =
=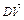 +
+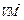 =-
=-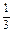 (a+b+c)+
(a+b+c)+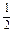
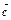
=
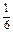 (-2a-2b+c).
(-2a-2b+c).∴|
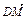 |=
|=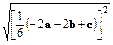 =
=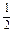 ,
,|
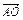 |=
|=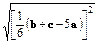 =
=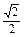 ,
,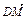 ·
·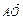 =
=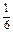 (-2a-2b+c)·
(-2a-2b+c)·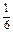 (b+c-5a)=
(b+c-5a)=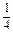 ,
,∴cos〈
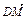 ,
,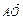 〉=
〉=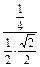 =
=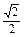 ,
,∵〈
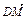 ,
,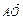 〉∈(0,
〉∈(0,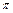 ),∴〈
),∴〈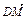 ,
, 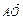 〉=45°.
〉=45°.
练习册系列答案
相关题目
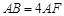 .
.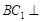 平面
平面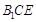 .
.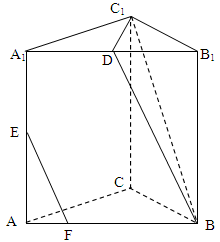
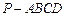 的底面
的底面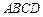 为一直角梯形,其中
为一直角梯形,其中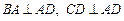 ,
,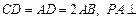 底面
底面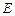 是
是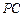 的中点.
的中点.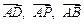 表示
表示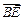 ,并判断直线
,并判断直线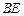 与平面
与平面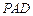 的位置关系;
的位置关系;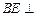 平面
平面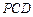 ,求异面直线
,求异面直线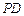 与
与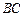 所成角的余弦值.
所成角的余弦值.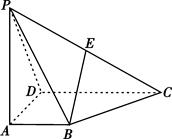
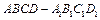 中,
中,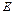 为
为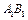 的中点,则异面直线
的中点,则异面直线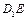 和
和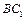 间的距离 .
间的距离 .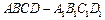 中,
中,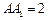 ,底面
,底面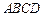 是直角梯形,
是直角梯形,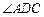 是直角,
是直角,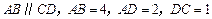 ,求异面直线
,求异面直线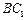 与
与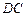 所成角的大小.
所成角的大小.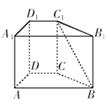
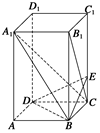 E是棱CC1上的点,且BE⊥B1C.
E是棱CC1上的点,且BE⊥B1C.