题目内容
10.将函数y=cosx的图象向右平移$\frac{π}{2}$个单位,得到函数y=f(x)的图象,则下列说法正确的是( )| A. | y=f(x)是偶函数 | B. | y=f(x)的周期为π | ||
| C. | y=f(x)的图象关于直线$x=\frac{π}{2}$对称 | D. | y=f(x)的图象关于点$(-\frac{π}{2},0)$对称 |
分析 由条件根据函数y=Asin(ωx+φ)的图象变换规律可得f(x)的解析式,利用正弦函数的图象和性质即可得解.
解答 解:由于把函数y=cosx的图象向右平移$\frac{π}{2}$个单位,得到函数y=f(x)=cos(x-$\frac{π}{2}$)=sinx的图象,
由正弦函数的图象和性质可知,y=f(x)是奇函数,故A错误;周期为2π,故B错误;由y=f(-$\frac{π}{2}$)=sin(-$\frac{π}{2}$)=-1≠0,故D错误;
由y=f($\frac{π}{2}$)=sin($\frac{π}{2}$)=1,故C正确.
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
19.已知a,b∈R,a2+2b2=1,则a-b的最小值为( )
| A. | -$\sqrt{5}$ | B. | -$\frac{\sqrt{6}}{2}$ | C. | -$\sqrt{6}$ | D. | -$\sqrt{2}$ |
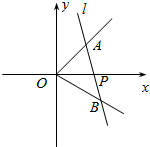 如图,射线OA、OB分别与x轴成45°角和30°角,过点P(1,0)作直线AB分别与OA、OB交于A、B.
如图,射线OA、OB分别与x轴成45°角和30°角,过点P(1,0)作直线AB分别与OA、OB交于A、B.