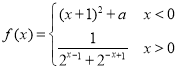题目内容
【题目】已知![]() ,
,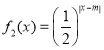 ,其中
,其中![]() .
.
(1)若![]() ,令函数
,令函数![]() ,解不等式
,解不等式![]() ;
;
(2)若![]() ,
,![]() ,求
,求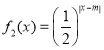 的值域;
的值域;
(3)设函数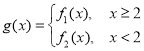 ,若对于任意大于等于2的实数
,若对于任意大于等于2的实数![]() ,总存在唯一的小于2的实数
,总存在唯一的小于2的实数![]() ,使得
,使得![]() 成立,试确定实数m的取值范围.
成立,试确定实数m的取值范围.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,值域为
时,值域为![]() ,当
,当![]() 时,值域为
时,值域为![]() ;(3)
;(3)![]()
【解析】
(1)先由导函数得出![]() 在
在![]() 上的单调性,再根据单调性解函数不等式即可;(2)先求出
上的单调性,再根据单调性解函数不等式即可;(2)先求出![]() 的范围,再根据指数函数
的范围,再根据指数函数![]() 的单调性求得值域;(3)首先对
的单调性求得值域;(3)首先对![]() 进行分类讨论,接下来研究函数
进行分类讨论,接下来研究函数![]() 的单调性,再由“总存在唯一的小于2的实数
的单调性,再由“总存在唯一的小于2的实数![]() ,使得
,使得![]() 成立”分别求出两函数的值域,使得
成立”分别求出两函数的值域,使得![]() 的值域为
的值域为![]() 的值域的子集,建立不等关系,解之即可.
的值域的子集,建立不等关系,解之即可.
(1)∵![]() ,
,![]() 时,
时,
![]() ,
,
则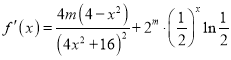
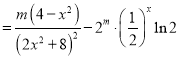 且
且![]() ,
,![]() ,
,
∴![]() ,∴函数
,∴函数![]() 为单调递减函数,
为单调递减函数,
又![]() ,
,![]() ,
,
∴![]() ,
,
整理得![]() ,解得
,解得![]() 或
或![]() ,
,
不等式的解集为![]() .
.
(2)∵![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,所以
,所以![]() 的值域为
的值域为![]() .
.
(3)①若![]() ,由
,由![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴![]() 不成立,
不成立,
②若![]() ,由
,由![]() 时,
时,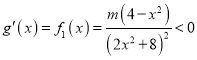 ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
从而![]() ,即
,即![]()
(![]() )若
)若![]() ,由于
,由于![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
从而![]() ,即
,即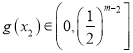 ,
,
要使![]() 成立,只需
成立,只需![]() ,
,
即![]() 成立即可,
成立即可,
由于函数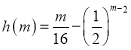 在
在![]() 上单调递增,且
上单调递增,且![]() ,
,
∴![]()
(![]() )若
)若![]() ,由于
,由于![]() 时,
时,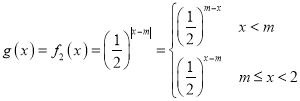 ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
从而![]() ,即
,即![]() ,
,
要使![]() 成立,只需
成立,只需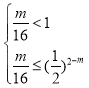 成立,
成立,
即![]() 成立即可.
成立即可.
由![]() ,可得
,可得![]() ,
,![]() 故当
故当![]() 时,
时,
![]() 恒成立.
恒成立.
综上所述:![]() 的取值范围是
的取值范围是![]() .
.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】垃圾种类可分为可回收垃圾,干垃圾,湿垃圾,有害垃圾,为调查中学生对垃圾分类的了解程度某调查小组随机抽取了某市的![]() 名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于
名高中生,请他们指出生活中若干项常见垃圾的种类,把能准确分类不少于![]() 项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
项的称为“比较了解”少于三项的称为“不太了解”调查结果如下:
|
|
|
|
|
|
| |
男生(人) |
|
|
|
|
|
|
|
女生(人) |
|
|
|
|
|
|
|
(1)完成如下![]() 列联表并判断是否有
列联表并判断是否有![]() 的把握认为了解垃圾分类与性别有关?
的把握认为了解垃圾分类与性别有关?
比较了解 | 不太了解 | 合计 | |
男生 | ________ | ________ | ________ |
女生 | ________ | ________ | ________ |
合计 | ________ | ________ | ________ |
p>
(2)抽取的![]() 名高中生中按照男、女生采用分层抽样的方法抽取
名高中生中按照男、女生采用分层抽样的方法抽取![]() 人的样本.
人的样本.
(i)求抽取的女生和男生的人数;
(ii)从![]() 人的样本中随机抽取两人,求两人都是女生的概率.
人的样本中随机抽取两人,求两人都是女生的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
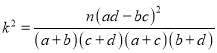 ,
,![]() .
.