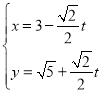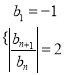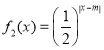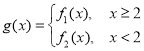Question

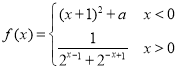【题目】已知，函数，若函数的图像上有且只有两对点关于轴对称，则的取值范围是________

Answer 1

【答案】

【解析】

运用对称性及单调性求得x＞0时，f（x）的最大值，再求得关于y轴对称的函数和图象，画出f（x）和g（x）的图象，结合图象求得仅有两个交点的a的范围．

令，

则是由向右平移1个单位得到的，

而是R上的偶函数，且在上单减，在上单增，

∴关于x=1对称，且在上单减，在上单增，

即当x＝1时，f1（x）min＝2，

∴当x＞0时，函数，关于x=1对称，且在上单增，在上单减，∴当x＞0时，；

∴的大致图象如图所示：

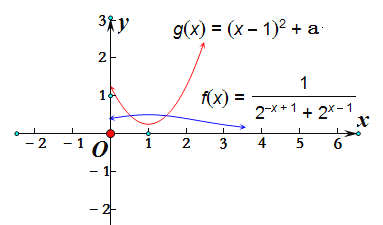
若f（x）图象仅有两对点关于y轴对称，

即f（x）（x＜0）的图象关于y轴对称的函数图象与f（x）（x＞0）仅有两个交点，

而当x＜0时，f（x）＝（x+1）2+a．

设其关于y轴对称的函数为g（x），

∴g（x）＝f（﹣x）＝（x﹣1）2+a（x＞0），∴g（x），

又当x=0时，，而当x=0时，（x﹣1）2+a+1，

当g（x）与f（x）仅有两个交点时，且

∴，

综上，a的取值范围是（，），

故答案为：（，）．