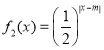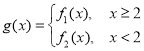Question

【题目】考虑下面两个定义域为（0，+∞）的函数f（x）的集合：对任何不同的两个正数，都有，=对任何不同的两个正数，都有

（1）已知，若，且，求实数和的取值范围

（2）已知，且的部分函数值由下表给出：

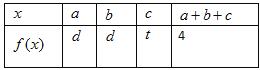
比较与4的大小关系

（3）对于定义域为的函数，若存在常数，使得不等式对任何都成立，则称为的上界，将中所有存在上界的函数组成的集合记作，判断是否存在常数，使得对任何和，都有，若存在，求出的最小值，若不存在，说明理由

Answer 1

【答案】（1）当a≥0，b＜0时，f（x）∈Ω1且f（x）Ω2；（2）2d+t＜4；（3）0．

【解析】

（1）根据：f（x）∈Ω1且f（x）Ω2，可利用二次函数的单调性可得a的范围，利用导数求出b的范围．

（2）由f（x）∈Ω1，取0＜x1＜x2＜x1+x2，可得．由表格可知：f（a）＝d，f（b）＝d，f（c）＝t，f（a+b+c）＝4，0＜a＜b＜c＜a+b+c，利用函数为增函数可得，再利用不等式的性质即可得出．

（3）根据增函数先证明f（x）≤0对x∈（0，+∞）成立．再证明f（x）＝0在（0，+∞）上无解．即可得出．

（1）由：对任何不同的两个正数，都有，=对任何不同的两个正数，都有，

可得函数y，y在（0，+∞）为增函数，

y2x2+2ax+b，若f（x）∈Ω1，则0，即a≥0

y2x+a，

y′＝2，

当b≥0，x＞0时，y′＞0，此时f（x）∈Ω2，不符合题意，舍去；

当b＜0时，令y′＝0，解得x，此时函数在x∈（0，+∞）有极值点，因此f（x）Ω2．

综上可得：当b＜0时，f（x）∈/span>Ω1且f（x）Ω2．

（2）由f（x）∈Ω1，若取0＜x1＜x2，

则．

由表格可知：f（a）＝d，f（b）＝d，f（c）＝t，f（a+b+c）＝4，

∵0＜a＜b＜c＜a+b+c，

∴，

∴d＜0，d，d，t，

∴2d+t=4.

（3）∵对任何f（x）∈T和x∈（0，+∞），都有f（x）＜M，

先证明f（x）≤0对x∈（0，+∞）成立．

假设存在x0∈（0，+∞），使得f（x0）＞0，

记m＞0

∵y是增函数．

∴当x＞x0时，m＞0，

∴f（x）＞mx2，

∴一定可以找到一个x1＞x0，使得f（x1）＞mx12＞k，

这与f（x）＜k 对x∈（0，+∞）成立矛盾．

即f（x）≤0对x∈（0，+∞）成立．

∴存在f（x）∈T，f（x）≤0对x∈（0，+∞）成立．

下面证明f（x）＝0在（0，+∞）上无解．

假设存在x2＞0，使得f（x2）＝0，

∵y是增函数．

一定存在x3＞x2＞0，使0，这与上面证明的结果矛盾．

∴f（x）＝0在（0，+∞）上无解．

综上，我们得到存在f（x）∈T，f（x）＜0对x∈（0，+∞）成立．

∴存在常数M≥0，使得存在f（x）∈T，x∈（0，+∞），有f（x）＜M成立．

又令f（x）（x＞0），则f（x）＜0对x∈（0，+∞）成立，

又有在（0，+∞）上是增函数，

∴f（x）∈T，

而任取常数k＜0，总可以找到一个xn＞0，使得x＞xn时，有f（x）＞k．

∴M的最小值为0．