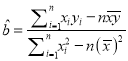题目内容
【题目】已知圆![]() 过点
过点![]() 和点
和点![]() ,且圆心
,且圆心![]() 在直线
在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作圆
作圆![]() 的切线,求切线方程.
的切线,求切线方程.
(3)设直线![]() ,且直线
,且直线![]() 被圆
被圆![]() 所截得的弦为
所截得的弦为![]() ,满足
,满足![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) x2+y2-6x+4y+4=0. (2) ![]() 或
或![]() .(3)y=x-1或y=x-4.
.(3)y=x-1或y=x-4.
【解析】试题分析:(1)设圆心C(a,b),由两点间距离公式及圆心在直线上,列出方程组,求出圆心坐标,进而求出圆半径,由此能求出圆C的方程.
(2)当切线的斜率k存在时,设过点(6,3)的切线方程为kx﹣y﹣6k+3=0,则圆心C(3,﹣2)到切线的距离d=![]() ,求出k,从而求出切线方程;当切线斜率k不存在时,切线方程为x=6,成立.由此能求出切线方程.
,求出k,从而求出切线方程;当切线斜率k不存在时,切线方程为x=6,成立.由此能求出切线方程.
(3)由题意得OA⊥OB,从而|OA|2+|OB|2=|AB|2,进而解得m=-1或m=-4,由此能求出直线l的方程.
试题解析:
(Ⅰ)设圆C的方程为x2+y2+Dx+Ey+F=0,
则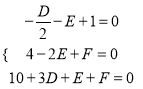 ,解得D=-6,E=4,F=4,
,解得D=-6,E=4,F=4,
所以圆C的方程为x2+y2-6x+4y+4=0.
(Ⅱ)圆C的方程为![]() ,
,
当斜率存在时,设切线方程为![]() ,则
,则
![]() ,解得
,解得![]() ,
,
所以切线方程为![]() ,即
,即![]() .
.
当斜率不存在时, ![]() .
.
所以所求的切线方程为![]() 或
或![]() .
.
(Ⅲ)直线l的方程为y=x+m.
设A(x1,y1),B(x2,y2),
则联立![]() 消去y得2x2+2(m-1)x+m2+4m+4=0,(*)
消去y得2x2+2(m-1)x+m2+4m+4=0,(*)
∴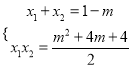 ∴y1y2=(x1+m)(x2+m)=x1x2+m
∴y1y2=(x1+m)(x2+m)=x1x2+m
∵∠AOB=90°,∴|OA|2+|OB|2=|AB|2,
∴![]() =(x1-x2)2+(y1-y2)2,
=(x1-x2)2+(y1-y2)2,
得x1x2+y1y2=0,∴2x1x2+m(x1+x2)+m2=0,
即m2+4m+4+m(1-m)+m2=0,解得m=-1或m=-4.
容易验证m=-1或m=-4时方程(*)有实根.
所以直线l的方程是y=x-1或y=x-4.

 阅读快车系列答案
阅读快车系列答案【题目】2016年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件,测量产品中的微量元素的含量(单位:毫克).下表是从乙厂抽取的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
(1)求乙厂生产的产品数量:
(2)当产品中的微量元素![]() 满足:
满足:![]() ,且
,且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数的分布列及数学期望.