题目内容
设函数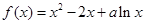 .
.
(1)若函数 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数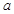 的取值范围;
的取值范围;
(2)求函数 的极值点.
的极值点.
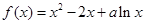 .
.(1)若函数
 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数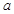 的取值范围;
的取值范围;(2)求函数
 的极值点.
的极值点.(1) (2)
(2)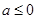 时,
时, 在
在 上有唯一的极小值点
上有唯一的极小值点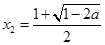 ;
;
 时,
时, 有一个极大值点
有一个极大值点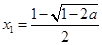 和一个极小值点
和一个极小值点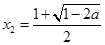 ;
; 时,函数
时,函数 在
在 上无极值点.
上无极值点.
 (2)
(2)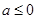 时,
时, 在
在 上有唯一的极小值点
上有唯一的极小值点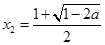 ;
; 时,
时, 有一个极大值点
有一个极大值点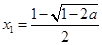 和一个极小值点
和一个极小值点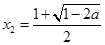 ;
; 时,函数
时,函数 在
在 上无极值点.
上无极值点.(1)先求导,可得 ,因为函数
,因为函数 是定义域上的单调函数,所以只能是
是定义域上的单调函数,所以只能是 上恒成立,也就是说函数f(x)只能是增函数,到此问题基本得解.
上恒成立,也就是说函数f(x)只能是增函数,到此问题基本得解.
(2)在(1)的基础上,可知当 时,
时, 的点是导数不变号的点,函数无极值点;然后再分
的点是导数不变号的点,函数无极值点;然后再分 和
和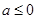 两种情况进一步研究.
两种情况进一步研究.
解:(1) ,若函数
,若函数 是定义域上的单调函数,
是定义域上的单调函数,
则只能 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立.,
上恒成立.,
 ,
,
令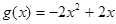 ,则
,则 ,可得
,可得 ,即只要
,即只要 .
.
(或令 ,则函数
,则函数 图象的对称轴方程是
图象的对称轴方程是 ,故只要
,故只要 恒成立,)
恒成立,)
(2)有(1)知当 时,
时, 的点是导数不变号的点,
的点是导数不变号的点,
故 时,函数无极值点;
时,函数无极值点;
当 时,
时, 的根是
的根是 ,
,
若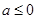 ,
, ,此时
,此时 ,
, ,且在
,且在 上
上 ,
,
在 上
上 ,故函数
,故函数 有唯一的极小值点
有唯一的极小值点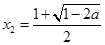 ;
;
当 时,
时, ,此时
,此时 ,
,
 在
在 都大于
都大于 ,
, 在
在 上小于
上小于 ,
,
此时 有一个极大值点
有一个极大值点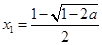 和一个极小值点
和一个极小值点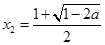 .
.
综上可知,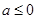 时,
时, 在
在 上有唯一的极小值点
上有唯一的极小值点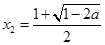 ;
;
 时,
时, 有一个极大值点
有一个极大值点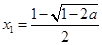 和一个极小值点
和一个极小值点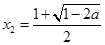 ;
; 时,函数
时,函数 在
在 上无极值点.
上无极值点.
 ,因为函数
,因为函数 是定义域上的单调函数,所以只能是
是定义域上的单调函数,所以只能是 上恒成立,也就是说函数f(x)只能是增函数,到此问题基本得解.
上恒成立,也就是说函数f(x)只能是增函数,到此问题基本得解.(2)在(1)的基础上,可知当
 时,
时, 的点是导数不变号的点,函数无极值点;然后再分
的点是导数不变号的点,函数无极值点;然后再分 和
和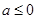 两种情况进一步研究.
两种情况进一步研究.解:(1)
 ,若函数
,若函数 是定义域上的单调函数,
是定义域上的单调函数,则只能
 在
在 上恒成立,即
上恒成立,即 在
在 上恒成立.,
上恒成立., ,
,令
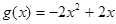 ,则
,则 ,可得
,可得 ,即只要
,即只要 .
.(或令
 ,则函数
,则函数 图象的对称轴方程是
图象的对称轴方程是 ,故只要
,故只要 恒成立,)
恒成立,) (2)有(1)知当
 时,
时, 的点是导数不变号的点,
的点是导数不变号的点,故
 时,函数无极值点;
时,函数无极值点;当
 时,
时, 的根是
的根是 ,
,若
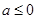 ,
, ,此时
,此时 ,
, ,且在
,且在 上
上 ,
,在
 上
上 ,故函数
,故函数 有唯一的极小值点
有唯一的极小值点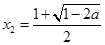 ;
; 当
 时,
时, ,此时
,此时 ,
, 在
在 都大于
都大于 ,
, 在
在 上小于
上小于 ,
,此时
 有一个极大值点
有一个极大值点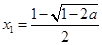 和一个极小值点
和一个极小值点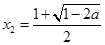 .
. 综上可知,
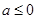 时,
时, 在
在 上有唯一的极小值点
上有唯一的极小值点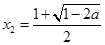 ;
; 时,
时, 有一个极大值点
有一个极大值点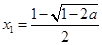 和一个极小值点
和一个极小值点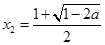 ;
; 时,函数
时,函数 在
在 上无极值点.
上无极值点.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
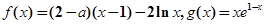 ,(
,(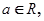 e为自然对数的底数)
e为自然对数的底数)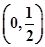 上无零点,求a的最小值;
上无零点,求a的最小值;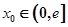 ,在
,在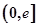 上总存在两个不同的
上总存在两个不同的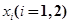 ,使得
,使得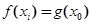 成立,求a的取值范围.
成立,求a的取值范围.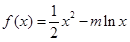 (m
(m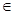 R)
R) 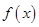 在
在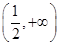 上单调递增,求实数
上单调递增,求实数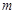 的取值范围;
的取值范围;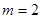 时,求函数
时,求函数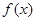 在
在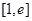 上的最大,最小值;
上的最大,最小值; .
. 是函数
是函数 在区间
在区间 上递增的充分而不必要的条件;
上递增的充分而不必要的条件; 时,满足
时,满足 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的导函数为
的导函数为 ,
, ,f(x)与x轴恰有一个交点,则
,f(x)与x轴恰有一个交点,则 的最小值为 ( )
的最小值为 ( ) 

 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减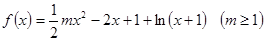 .
.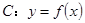 在点
在点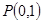 处的切线
处的切线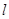 与曲线
与曲线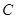 有且只有一个公共点,求
有且只有一个公共点,求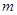 的值;
的值;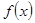 存在单调递减区间
存在单调递减区间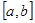 ,并求出单调递减区间的长度
,并求出单调递减区间的长度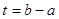 的取值范围.
的取值范围. 在区间
在区间 上是减函数,则
上是减函数,则 的最小值是( )
的最小值是( )  是减函数的区间为( )
是减函数的区间为( )

