题目内容
(本小题满分14分) 已知:三次函数 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
(1)求函数f (x)的解析式;
(2)求函数f (x)在区间[-2,2]的最值。
 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减(1)求函数f (x)的解析式;
|
(1)
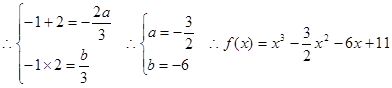 ;
;
(2)当X=-1时,Ymax=f(-1)=14.5, 当X=2时,Ymin=1 。
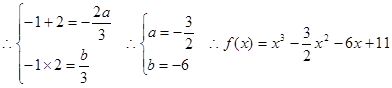 ;
;(2)当X=-1时,Ymax=f(-1)=14.5, 当X=2时,Ymin=1 。
本试题主要是考查了导数在研究函数中的运用
(1)因为三次函数 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减
可知函数在x=-1,x=2处1取得极值,联立方程组得到参数a,b的值。
(2)在第一问的基础上可以求解得到函数的 极值,和端点值,进而得到最值。
解:(1)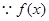 在
在 上单增,(-1,2)上单减
上单增,(-1,2)上单减
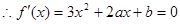 有两根-1,2
有两根-1,2
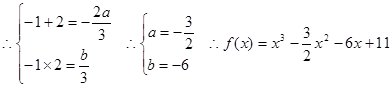 …………6分
…………6分
(2)当X=-1时,Ymax=f(-1)=14.5, 当X=2时,Ymin=1 (14分)
(1)因为三次函数
 ,在
,在 上单调递增,在
上单调递增,在 上单调递减
上单调递减可知函数在x=-1,x=2处1取得极值,联立方程组得到参数a,b的值。
(2)在第一问的基础上可以求解得到函数的 极值,和端点值,进而得到最值。
解:(1)
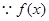 在
在 上单增,(-1,2)上单减
上单增,(-1,2)上单减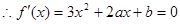 有两根-1,2
有两根-1,2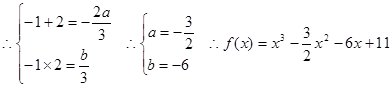 …………6分
…………6分(2)当X=-1时,Ymax=f(-1)=14.5, 当X=2时,Ymin=1 (14分)

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
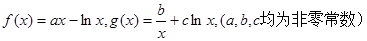 .
.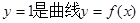 的切线,函数
的切线,函数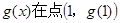 处取得极值1,求
处取得极值1,求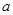 ,
,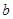 ,
,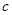 的值;
的值; 证明:
证明: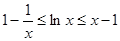 ;
; 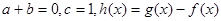 ,且函数
,且函数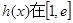 上单调递增,
上单调递增,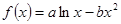 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为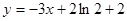 .
.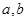 的值;
的值;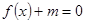 在
在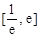 内有两个不等实根,求
内有两个不等实根,求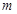 的取值范围(其中
的取值范围(其中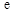 为自然对数的底);
为自然对数的底);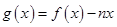 ,如果
,如果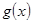 图象与
图象与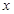 轴交于
轴交于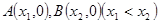 ,AB中点为
,AB中点为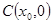 ,求证:
,求证: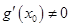 .
.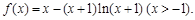
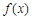 的单调区间;
的单调区间;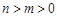 时,
时,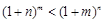 ;
;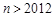 ,且
,且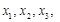 …,
…,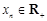 ,
,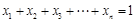 时,
时,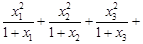 …
…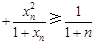
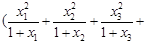 …
…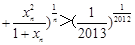 .
.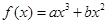 的图像经过点
的图像经过点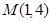 ,曲线在点
,曲线在点 处的切线恰好与直线
处的切线恰好与直线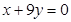 垂直.
垂直. 的值;
的值;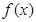 在区间
在区间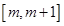 上单调递增,求实数
上单调递增,求实数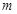 的取值范围.
的取值范围.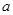 为常数,函数
为常数,函数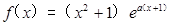 (
(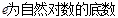 )。
)。 在区间(-2,-1)上为减函数,求实数
在区间(-2,-1)上为减函数,求实数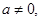 记函数
记函数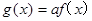 ,已知函数
,已知函数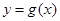 在区间
在区间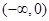 内有两个极值点
内有两个极值点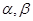 ,且
,且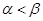 ,若对于满足条件的任意实数
,若对于满足条件的任意实数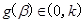 (
(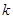 为正整数),求
为正整数),求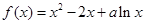 .
. 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数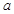 的取值范围;
的取值范围;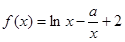 。
。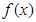 的单调区间;
的单调区间;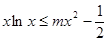 在
在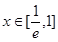 上恒成立,求
上恒成立,求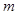 的取值范围。
的取值范围。