题目内容
6.在△ABC中,a=3,b=2$\sqrt{6}$,∠B=2∠A.(Ⅰ)求cosA的值;
(Ⅱ)求c的值.
分析 ( I)由正弦定理得$\frac{3}{sinA}=\frac{{2\sqrt{6}}}{sin2A}$,结合二倍角公式及sinA≠0即可得解.
( II)由( I)可求sinA,又根据∠B=2∠A,可求cosB,可求sinB,利用三角形内角和定理及两角和的正弦函数公式即可得sinC,利用正弦定理即可得解.
解答 解:( I)因为a=3,b=2$\sqrt{6}$,∠B=2∠A.
所以在△ABC中,由正弦定理得$\frac{3}{sinA}=\frac{{2\sqrt{6}}}{sin2A}$.
所以$\frac{2sinAcosA}{sinA}=\frac{{2\sqrt{6}}}{3}$.
故$cosA=\frac{{\sqrt{6}}}{3}$.
( II)由( I)知$cosA=\frac{{\sqrt{6}}}{3}$,
所以$sinA=\sqrt{1-{{cos}^2}A}=\frac{{\sqrt{3}}}{3}$.
又因为∠B=2∠A,
所以$cosB=2{cos^2}A-1=\frac{1}{3}$.
所以$sinB=\sqrt{1-{{cos}^2}B}=\frac{{2\sqrt{2}}}{3}$.
在△ABC中,$sinC=sin(A+B)=sinAcosB+cosAsinB=\frac{{5\sqrt{3}}}{9}$.
所以$c=\frac{asinC}{sinA}=5$.
点评 本题主要考查了正弦定理,同角三角函数关系式,两角和的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
19.以下各点中,在不等式组$\left\{\begin{array}{l}{x-2y+5>0}\\{x-y+3≤0}\end{array}\right.$表示的平面区域中的点是( )
| A. | (-2,1) | B. | (2,1) | C. | (-1,2) | D. | (1,2) |
17.当直线y=kx与曲线y=|x|-|x-2|有3个公共点时,实数k的取值范围是( )
| A. | (0,1) | B. | (0,1] | C. | (1,+∞) | D. | [1,+∞) |
18.已知△ABC满足|AB|=3,|AC|=4,O是△ABC所在平面内一点,满足|$\overrightarrow{AO}|=|\overrightarrow{BO}|=|\overrightarrow{CO}$|,且$\overrightarrow{AO}=λ\overrightarrow{AB}+\frac{1-λ}{2}\overrightarrow{AC}$(λ∈R),则cos∠BAC=( )
| A. | $\frac{2}{3}$或$\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
16.一排九个坐位有六个人坐,若每个空位两边都坐有人,共有( )种不同的坐法.
| A. | 7200 | B. | 3600 | C. | 2400 | D. | 1200 |
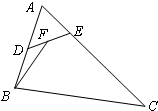 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )