题目内容
15.观察下列不等式1>$\frac{1}{2}$,1+$\frac{1}{2}$+$\frac{1}{3}$>1,1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{7}$>$\frac{3}{2}$,1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{15}$>2,…,则可归纳出一般性的不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$>$\frac{n}{2}$.分析 由已知的式子可发现左边为正整数的倒数和,第一个式子一个数,第二个式子3个数,第三个式子7个数,第四个式子15个数,可猜测第n个式子应为2n-1个数;式子右侧为$\frac{1}{2}$,1,$\frac{3}{2}$,2,…,即为$\frac{1}{2}$,$\frac{2}{2}$,$\frac{3}{2}$,$\frac{4}{2}$,…,故第n个应为$\frac{n}{2}$.
解答 解:观察已知中的不等式:
1>$\frac{1}{2}$,
1+$\frac{1}{2}$+$\frac{1}{3}$>1,
1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$+$\frac{1}{6}$+$\frac{1}{7}$>$\frac{3}{2}$,
1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{15}$>2,
…,
归纳可得:第n个不等式为:1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$>$\frac{n}{2}$,
故答案为:1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{{2}^{n}-1}$>$\frac{n}{2}$
点评 归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
3.f(x)是定义在[-3,3]上的奇函数,且x>0时,f′(x)cosx<f(x)sinx则不等式f(x)cosx>0的解集是( )
| A. | [-3,0] | B. | $(-\frac{π}{2},0)∪(\frac{π}{2},3]$ | C. | $[-3,-\frac{π}{2})∪(\frac{π}{2},3]$ | D. | $[-3,-\frac{π}{2})∪(0,\frac{π}{2})$ |
5.已知A${\;}_{n}^{2}$=7A${\;}_{n-4}^{2}$,则n的值为( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |

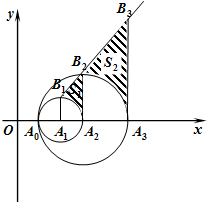 如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).
如图,在平面直角坐标系xOy中,设a1=2,有一组圆心在x轴正半轴上的圆An(n=1,2,…)与x轴的交点分别为A0(1,0)和An+1(an+1,0).过圆心An作垂直于x轴的直线ln,在第一象限与圆An交于点Bn(an,bn).