题目内容
已知以点C (t, 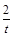 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
(1)求证:△OAB的面积为定值;
(2)设直线y= –2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y –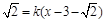 的距离为
的距离为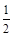 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
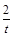 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.(1)求证:△OAB的面积为定值;
(2)设直线y= –2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y –
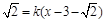 的距离为
的距离为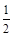 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.(1)∵圆C过原点O,∴OC2=t2+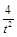 则圆C的方程为
则圆C的方程为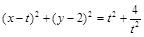
令x=0,得y1=0,y2=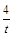 ;令y=0得x1=0,x2=2t,即A(2t,0) B(0,
;令y=0得x1=0,x2=2t,即A(2t,0) B(0, 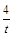 )
)
∴S△OAB=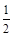 OA×OB=
OA×OB=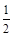 |
|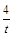 |×|2t|=4.……4分
|×|2t|=4.……4分
即△OAB的面积为定值
(2)∵|OM|=|ON|,|CM|=|CN|,∴OC垂直平分线段MN.
∵KMN =" –" 2 ∴KOC=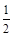
∴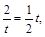 解得t=2或t = –2.
解得t=2或t = –2.
当t=2时,圆心C的坐标为(2,1)半径OC=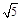 ,此时圆心到直线y= –2x+4的距离d=
,此时圆心到直线y= –2x+4的距离d=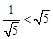 ,即圆C与直线y= –2x+4相交于两点。
,即圆C与直线y= –2x+4相交于两点。
当t=-2时,圆心C的坐标为(–2,–1)半径OC=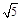
此时圆心到直线y= –2x+4的距离d=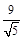 >
>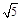 , 即圆C与直线y= –2x+4不相交,
, 即圆C与直线y= –2x+4不相交,
∴t= –2不合题意,舍去.∴圆C的方程为(x –2)2+(y –1)2=5.……9分
(3)半径OC=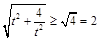 .当且仅当t=
.当且仅当t=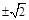 时取等号 ∵t>0 ∴t=
时取等号 ∵t>0 ∴t=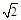 .
.
此时圆心坐标为C(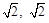 )半径为2.
)半径为2.
若圆C上至少有三个不同的点到直线l:y –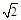 =k(x –3 –
=k(x –3 –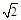 )的距离为
)的距离为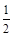 .
.
则圆心C到直线的距离d≤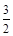 .即:
.即: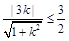 所以–
所以– 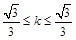 .
.
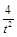 则圆C的方程为
则圆C的方程为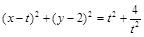
令x=0,得y1=0,y2=
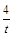 ;令y=0得x1=0,x2=2t,即A(2t,0) B(0,
;令y=0得x1=0,x2=2t,即A(2t,0) B(0, 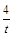 )
)∴S△OAB=
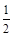 OA×OB=
OA×OB=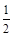 |
|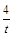 |×|2t|=4.……4分
|×|2t|=4.……4分即△OAB的面积为定值
(2)∵|OM|=|ON|,|CM|=|CN|,∴OC垂直平分线段MN.
∵KMN =" –" 2 ∴KOC=
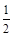
∴
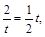 解得t=2或t = –2.
解得t=2或t = –2.当t=2时,圆心C的坐标为(2,1)半径OC=
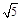 ,此时圆心到直线y= –2x+4的距离d=
,此时圆心到直线y= –2x+4的距离d=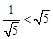 ,即圆C与直线y= –2x+4相交于两点。
,即圆C与直线y= –2x+4相交于两点。 当t=-2时,圆心C的坐标为(–2,–1)半径OC=
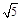
此时圆心到直线y= –2x+4的距离d=
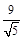 >
>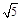 , 即圆C与直线y= –2x+4不相交,
, 即圆C与直线y= –2x+4不相交,∴t= –2不合题意,舍去.∴圆C的方程为(x –2)2+(y –1)2=5.……9分
(3)半径OC=
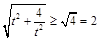 .当且仅当t=
.当且仅当t=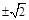 时取等号 ∵t>0 ∴t=
时取等号 ∵t>0 ∴t=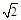 .
.此时圆心坐标为C(
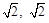 )半径为2.
)半径为2.若圆C上至少有三个不同的点到直线l:y –
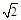 =k(x –3 –
=k(x –3 –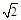 )的距离为
)的距离为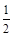 .
.则圆心C到直线的距离d≤
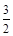 .即:
.即: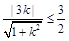 所以–
所以– 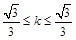 .
.略

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
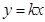 分抛物线
分抛物线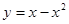 与
与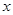 轴所围成图形为面积相等的两个部分,求
轴所围成图形为面积相等的两个部分,求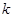 的值.
的值.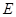 :
: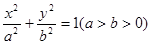 的左焦点
的左焦点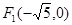 ,若椭圆上存在一点
,若椭圆上存在一点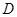 ,满足以椭圆短轴为直径的圆与线段
,满足以椭圆短轴为直径的圆与线段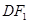 相切于线段
相切于线段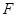 .
.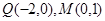 及椭圆
及椭圆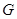 :
: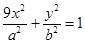 ,过点
,过点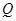 作斜率为
作斜率为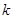 的直线
的直线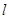 交椭圆
交椭圆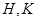 两点,设线段
两点,设线段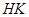 的中点为
的中点为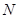 ,连结
,连结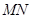 ,试问当
,试问当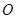 的直线交椭圆
的直线交椭圆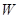 :
: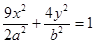 于
于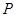 、
、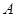 两点,其中
两点,其中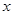 轴的垂线,垂足为
轴的垂线,垂足为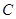 ,连结
,连结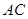 并延长交椭圆
并延长交椭圆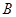 ,求证:
,求证: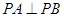
 |=2,O为AB中点,直线
|=2,O为AB中点,直线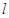 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与
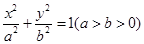 的离心率为
的离心率为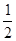 ,短轴的一个端点到右焦点的距离为2,
,短轴的一个端点到右焦点的距离为2, 求椭圆
求椭圆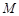 的方程;
的方程;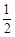 的直线
的直线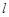 与椭圆
与椭圆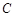 、
、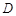 两点,点
两点,点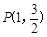 为椭圆
为椭圆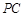 的斜率为
的斜率为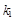 ,直线
,直线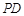 的斜率为
的斜率为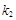 ,试问:
,试问: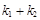 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.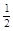 被椭圆x2+4y2=4截得的弦长为 。
被椭圆x2+4y2=4截得的弦长为 。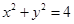 上任取一点
上任取一点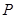 ,过点
,过点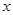 轴的垂线段
轴的垂线段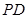 ,
,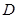 为垂足,当点
为垂足,当点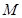 的轨迹为曲线
的轨迹为曲线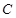
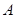
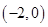 的直线
的直线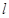 与曲线
与曲线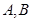 , 点
, 点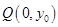 在线段
在线段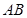 的垂直平分线上,且
的垂直平分线上,且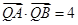 ,求
,求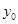 的值
的值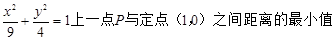 ( )。
( )。 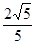
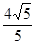
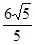
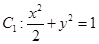 ,抛物线
,抛物线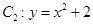 ,点
,点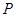 是
是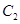 上的动点,过点
上的动点,过点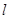 ,交椭圆
,交椭圆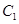 于
于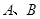 两点,
两点,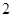 时,求
时,求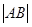 ;
;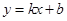 ,当
,当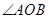 是锐角时,求
是锐角时,求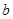 的取值范围.
的取值范围.