题目内容
已知椭圆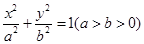 的离心率为
的离心率为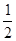 ,短轴的一个端点到右焦点的距离为2,
,短轴的一个端点到右焦点的距离为2,
(1)试 求椭圆
求椭圆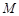 的方程;
的方程;
(2)若斜率为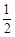 的直线
的直线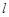 与椭圆
与椭圆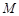 交于
交于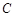 、
、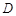 两点,点
两点,点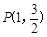 为椭圆
为椭圆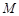 上一点,记直线
上一点,记直线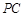 的斜率为
的斜率为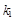 ,直线
,直线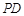 的斜率为
的斜率为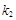 ,试问:
,试问: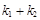 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
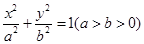 的离心率为
的离心率为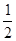 ,短轴的一个端点到右焦点的距离为2,
,短轴的一个端点到右焦点的距离为2,(1)试
 求椭圆
求椭圆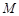 的方程;
的方程;(2)若斜率为
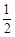 的直线
的直线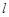 与椭圆
与椭圆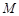 交于
交于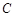 、
、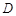 两点,点
两点,点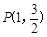 为椭圆
为椭圆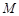 上一点,记直线
上一点,记直线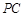 的斜率为
的斜率为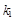 ,直线
,直线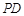 的斜率为
的斜率为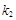 ,试问:
,试问: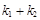 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.(1) .
. 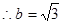 ,椭圆
,椭圆 的方程为
的方程为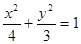
 ……4分
……4分
(2)设直线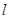 的方程为:
的方程为: ,
,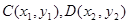
联立直线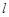 的方程与椭圆方程得:
的方程与椭圆方程得:

(1)代入(2)得:
化简得: ………(3) ……………6分
………(3) ……………6分
当 时,即,
时,即,
即 时,直线
时,直线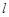 与椭圆有两交点, ………………7分
与椭圆有两交点, ………………7分
由韦达定理得: , ………………8分
, ………………8分
所以, ,
,  ………………10分
………………10分
则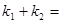

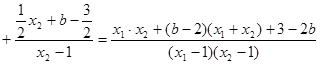
 ,
, 。
。
 .
. 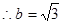 ,椭圆
,椭圆 的方程为
的方程为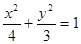
 ……4分
……4分(2)设直线
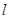 的方程为:
的方程为: ,
,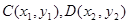
联立直线
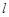 的方程与椭圆方程得:
的方程与椭圆方程得:
(1)代入(2)得:

化简得:
 ………(3) ……………6分
………(3) ……………6分当
 时,即,
时,即,
即
 时,直线
时,直线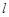 与椭圆有两交点, ………………7分
与椭圆有两交点, ………………7分由韦达定理得:
 , ………………8分
, ………………8分所以,
 ,
,  ………………10分
………………10分则
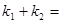

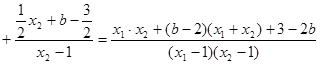
 ,
, 。
。略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
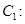
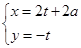 (
(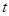 为参数),曲线
为参数),曲线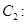
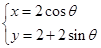 (
(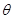 为参数).若曲线
为参数).若曲线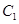 、
、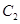 有公共点,则实数
有公共点,则实数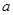 的取值范围_____.
的取值范围_____.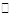 O方程为
O方程为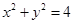 ,点P在圆上,点D在x轴上,点M在DP延长线上,
,点P在圆上,点D在x轴上,点M在DP延长线上,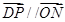 .且
.且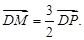
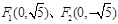 ,若过F1的直线交(I)中曲线C于A、B两点,求
,若过F1的直线交(I)中曲线C于A、B两点,求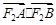 的取值范围.
的取值范围.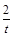 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.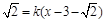 的距离为
的距离为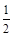 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.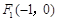 、
、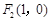 两点的距离之和等于2,则动点M的轨迹是椭圆;②在平面内,给出点
两点的距离之和等于2,则动点M的轨迹是椭圆;②在平面内,给出点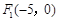 、
、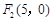 ,若动点P满足
,若动点P满足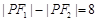 ,则动点P的轨迹是双曲线;③在平面内,若动点Q到点
,则动点P的轨迹是双曲线;③在平面内,若动点Q到点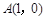 和到直线
和到直线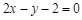 的距离相等,则动点Q的轨迹是抛物线。其中正确的命题有( )
的距离相等,则动点Q的轨迹是抛物线。其中正确的命题有( )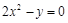 上移动,则点A(0,– 1)与点P连线中点的轨迹方程是_____________
上移动,则点A(0,– 1)与点P连线中点的轨迹方程是_____________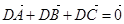 ;②|
;②|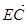 |=
|=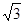 |
|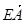 |=
|=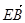 |③
|③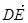 与
与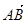 共线.
共线.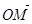 ·
·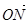 =0,求直线l的方程.
=0,求直线l的方程.