题目内容
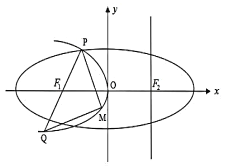
【题目】如图,设抛物线![]() 的准线
的准线![]() 与
与![]() 轴交于椭圆
轴交于椭圆![]() 的右焦点
的右焦点![]() 为
为![]() 的左焦点.椭圆的离心率为
的左焦点.椭圆的离心率为![]() ,抛物线
,抛物线![]() 与椭圆
与椭圆![]() 交于
交于![]() 轴上方一点
轴上方一点![]() ,连接
,连接![]() 并延长其交
并延长其交![]() 于点
于点![]() ,
, ![]() 为
为![]() 上一动点,且在
上一动点,且在![]() 之间移动.
之间移动.
(1)当![]() 取最小值时,求
取最小值时,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的边长恰好是三个连续的自然数,当
的边长恰好是三个连续的自然数,当![]() 面积取最大值时,求面积最大值以及此时直线
面积取最大值时,求面积最大值以及此时直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]() 的面积最大值为
的面积最大值为![]() .此时
.此时![]() .
.
【解析】试题分析:(1)由椭圆的性质可得![]() ,故可得
,故可得![]() ,故而可求得
,故而可求得![]() 和
和![]() 的方程;(2)因为
的方程;(2)因为![]() ,则
,则![]() ,设椭圆的标准方程为
,设椭圆的标准方程为![]() ,联立抛物线与椭圆的方程可得
,联立抛物线与椭圆的方程可得![]() ,得
,得![]() 代入抛物线方程得
代入抛物线方程得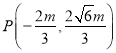 ,可得
,可得![]() ,可得直线与抛物线的方程,联立得
,可得直线与抛物线的方程,联立得![]() ,求出点到直线的距离,结合面积公式可得最值.
,求出点到直线的距离,结合面积公式可得最值.
试题解析:(1)因为![]() ,则
,则![]() ,所以
,所以![]() 取最小值时
取最小值时![]() ,
,
此时抛物线![]() ,此时
,此时![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() ;
;
(2)因为![]() ,则
,则![]() ,设椭圆的标准方程为
,设椭圆的标准方程为![]() ,
,
![]() 由
由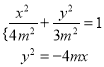 得
得![]() ,所以
,所以![]() 或
或![]() (舍去),代入抛物线方程得
(舍去),代入抛物线方程得![]() ,即
,即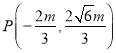 ,
,
于是![]() ,又
,又![]() 的边长恰好是三个连续的自然数,所以
的边长恰好是三个连续的自然数,所以![]() .此时抛物线方程为
.此时抛物线方程为![]() ,
, ![]() ,则直线
,则直线![]() 的方程为
的方程为![]() .联立
.联立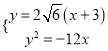 ,得
,得![]() 或
或![]() (舍去),于是
(舍去),于是![]() .所以
.所以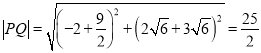 ,
,
设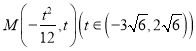 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则 ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 的面积最大值为
的面积最大值为![]() .此时
.此时![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:

其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如下表所示)
(单位:岁),并制作了对照表(如下表所示)
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为55岁观众周均学习成语知识时间.
,并预测年龄为55岁观众周均学习成语知识时间.
参考公式: 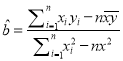 ,
, ![]() .
.