题目内容
【题目】已知定点![]() ,定直线
,定直线![]() :
: ![]() ,动圆
,动圆![]() 过点
过点![]() ,且与直线
,且与直线![]() 相切.
相切.
(Ⅰ)求动圆![]() 的圆心轨迹
的圆心轨迹![]() 的方程;
的方程;
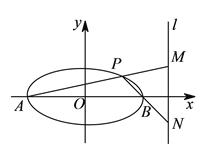
(Ⅱ)过点![]() 的直线与曲线
的直线与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,分别过点
两点,分别过点![]() ,
, ![]() 作曲线
作曲线![]() 的切线
的切线![]() ,
, ![]() ,两条切线相交于点
,两条切线相交于点![]() ,求
,求![]() 外接圆面积的最小值.
外接圆面积的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时线段
时线段![]() 最短,最短长度为4,此时圆的面积最小,最小面积为
最短,最短长度为4,此时圆的面积最小,最小面积为![]() .
.
【解析】试题分析:(Ⅰ)设![]() ,由
,由![]() 化简即可得结论;(Ⅱ)由题意
化简即可得结论;(Ⅱ)由题意![]() 的外接圆直径是线段
的外接圆直径是线段![]() ,设
,设![]() :
: ![]() ,与
,与 ![]() 联立得
联立得![]() ,从而得
,从而得![]() ,
, ![]() 时线段
时线段![]() 最短,最短长度为4,此时圆的面积最小,最小面积为
最短,最短长度为4,此时圆的面积最小,最小面积为![]() .
.
试题解析:(Ⅰ)设点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,依题意
,依题意![]() .
.
设![]() ,则有
,则有![]()
![]() .
.
化简得![]() .
.
所以点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() :
: ![]() ,
,
代入![]() 中,得
中,得![]() .
.
设![]() ,
, ![]() ,
,
则![]() ,
, ![]() .
.
所以![]()
![]() .
.
因为![]() :
: ![]() ,即
,即![]() ,所以
,所以![]() .
.
所以直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
因为![]() ,
,
所以![]() ,即
,即![]() 为直角三角形.
为直角三角形.
所以![]() 的外接圆的圆心为线段
的外接圆的圆心为线段![]() 的中点,线段
的中点,线段![]() 是直径.
是直径.
因为![]() ,
,
所以当![]() 时线段
时线段![]() 最短,最短长度为4,此时圆的面积最小,最小面积为
最短,最短长度为4,此时圆的面积最小,最小面积为![]() .
.
【方法点晴】本题主要考查直接法求轨迹方程、点到直线的距离公式及三角形面积公式,属于难题.求轨迹方程的常见方法有:①直接法,设出动点的坐标![]() ,根据题意列出关于
,根据题意列出关于![]() 的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把
的等式即可;②定义法,根据题意动点符合已知曲线的定义,直接求出方程;③参数法,把![]() 分别用第三个变量表示,消去参数即可;④逆代法,将
分别用第三个变量表示,消去参数即可;④逆代法,将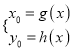 代入
代入![]() .本题(Ⅰ)就是利用方法①求圆心轨迹方程的.
.本题(Ⅰ)就是利用方法①求圆心轨迹方程的.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目