题目内容
【题目】如图,在正方体![]() 中,
中,![]() 、
、![]() 为棱
为棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:平面![]() 平面
平面![]() .
.
(Ⅲ)若正方体棱长为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.

【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)根据三角形中位线性质得EF//BD,再根据平行四边形性质得![]() ,从而有
,从而有![]() ,再根据线面平行判定定理得
,再根据线面平行判定定理得![]() 平面
平面![]() (2)分析可得关键证
(2)分析可得关键证![]() 平面
平面![]() ,这可由正方形性质得
,这可由正方形性质得![]() ,由正方体性质得
,由正方体性质得![]() 平面
平面![]() ,即得
,即得![]() ,最后根据线面垂直判定定理以及面面垂直判定定理证得结论(3)
,最后根据线面垂直判定定理以及面面垂直判定定理证得结论(3)![]() ,三棱锥高为
,三棱锥高为![]() ,再利用三棱锥体积公式可得体积
,再利用三棱锥体积公式可得体积
试题解析:(Ⅰ)
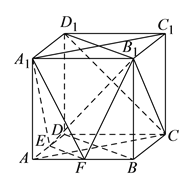
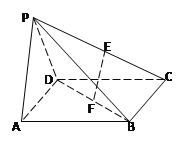
证明:连接![]() ,
,
∵![]() 且
且![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
又∵![]() 、
、![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)证明:在正方体![]() 中,
中,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅲ)![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示:

其中一个数字被污损.
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对成语知识的学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了4位观众的周均学习成语知识的时间![]() (单位:小时)与年龄
(单位:小时)与年龄![]() (单位:岁),并制作了对照表(如下表所示)
(单位:岁),并制作了对照表(如下表所示)
年龄 | 20 | 30 | 40 | 50 |
周均学习成语知识时间 | 2.5 | 3 | 4 | 4.5 |
由表中数据,试求线性回归方程![]() ,并预测年龄为55岁观众周均学习成语知识时间.
,并预测年龄为55岁观众周均学习成语知识时间.
参考公式: 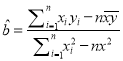 ,
, ![]() .
.