题目内容
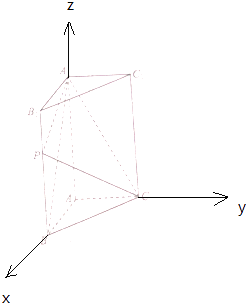
【题目】如图,在直三棱柱ABC﹣A1B1C1中,底面△ABC是直角三角形,AB=AC=1,点P是棱BB1上一点,满足 ![]() (0≤λ≤1).
(0≤λ≤1). 
(1)若λ= ![]() ,求直线PC与平面A1BC所成角的正弦值;
,求直线PC与平面A1BC所成角的正弦值;
(2)若二面角P﹣A1C﹣B的正弦值为 ![]() ,求λ的值.
,求λ的值.
【答案】
(1)解:以A为坐标原点O,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,
建立空间直角坐标系O﹣xyz.
∵AB=AC=1,AA1=2,则A(0,0,0),B(1,0,0),C(0,1,0),
A1(0,0,2),B1(1,0,2),P(1,0,2λ)
由 ![]() 得,
得, ![]() ,
, ![]() ,
, ![]() ,
,
设平面A1BC的法向量为 ![]() =(x1,y1,z1),由
=(x1,y1,z1),由 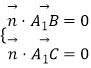 ,得
,得 ![]()
取z1=1,则x1=y1=2,从而平面A1BC的一个法向量为 ![]() =(2,2,1).
=(2,2,1).
设直线PC与平面A1BC所成的角为θ,
则sinθ=|cos< ![]() ,
, ![]() >|=
>|=  =
= ![]() ,
,
∴直线PC与平面A1BC所成的角的正弦值为 ![]()
(2)解:设平面PA1C的法向量为 ![]() =(x2,y2,z2),
=(x2,y2,z2), ![]() ,
,
由 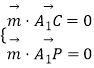 ,得
,得 ![]()
取z2=1,则x2=2﹣2λ,y2=2,平面PA1C的法向量为 ![]() =(2﹣2λ,2,1).
=(2﹣2λ,2,1).
则cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
又∵二面角P﹣A1C﹣B的正弦值为 ![]() ,∴
,∴ ![]()
化简得λ2+8λ﹣9=0,解得λ=1或λ=﹣9(舍去),
故λ的值为1.
【解析】(1)以A为坐标原点O,分别以AB,AC,AA1所在直线为x轴、y轴、z轴,建立空间直角坐标系O﹣xyz,利用向量法能求出直线PC与平面A1BC所成的角的正弦值.(2)求出平面PA1C的法向量和平面PA1C的法向量,利用向量法能求出λ的值.
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则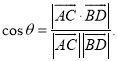 .
.

 阅读快车系列答案
阅读快车系列答案【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |


