题目内容
(本小题满分12分) 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是
 ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队,B队最后所得总分分别为 .
.
(1)求 的概率分布列;
的概率分布列;
(2)求 ,
, .
.
 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是  ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下:| 对阵队员 |  队队员胜的概率 队队员胜的概率 |  队队员负的概率 队队员负的概率 |
 对 对 |  |  |
 对 对 |  |  |
 对 对 |  |  |
现按表中对阵方式出场,每场胜队得1分,负队得0分,设A队,B队最后所得总分分别为
 .
.(1)求
 的概率分布列;
的概率分布列;(2)求
 ,
, .
.(1)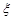 的分布列为
的分布列为
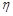 的分布列为
的分布列为
(2)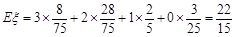 ,
,
因为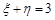 ,所以
,所以 .
.
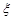 的分布列为
的分布列为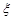 | 3 | 2 | 1 | 0 |
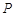 | 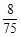 | 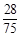 |  | 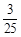 |
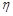 的分布列为
的分布列为| 0 | 1 | 2 | 3 |
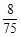 | 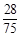 |  | 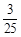 |
(2)
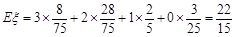 ,
,因为
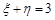 ,所以
,所以 .
.本试题主要是考查了独立事件概率的乘法公式的运用以及分布列的求解和数学期望值的运算。
(1)由于 的可能取值分别为3,2,1,0.分别分情况讨论得到各自的概率值即可。
的可能取值分别为3,2,1,0.分别分情况讨论得到各自的概率值即可。
(2)在第一问的基础上得到分布列,结合数学期望公式求解得到。
解:(1) 的可能取值分别为3,2,1,0.
的可能取值分别为3,2,1,0.
 ;
;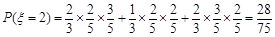 ;
;
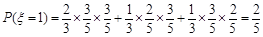 ;
;
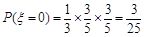 .
.
由题意知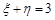 ,
,
所以 ;
;
 ;
;
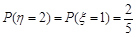 ;
;
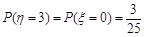 .
.
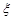 的分布列为
的分布列为
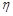 的分布列为
的分布列为
(2)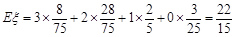 ,
,
因为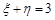 ,所以
,所以 .
.
(1)由于
 的可能取值分别为3,2,1,0.分别分情况讨论得到各自的概率值即可。
的可能取值分别为3,2,1,0.分别分情况讨论得到各自的概率值即可。(2)在第一问的基础上得到分布列,结合数学期望公式求解得到。
解:(1)
 的可能取值分别为3,2,1,0.
的可能取值分别为3,2,1,0. ;
;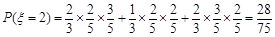 ;
;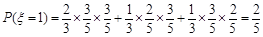 ;
;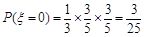 .
.由题意知
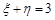 ,
,所以
 ;
; ;
;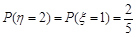 ;
;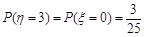 .
.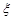 的分布列为
的分布列为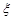 | 3 | 2 | 1 | 0 |
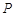 | 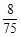 | 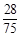 |  | 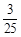 |
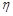 的分布列为
的分布列为| 0 | 1 | 2 | 3 |
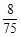 | 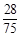 |  | 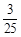 |
(2)
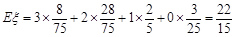 ,
,因为
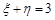 ,所以
,所以 .
.
练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
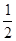 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。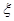 为与桌面接触的3个面上的3个数字中最大值与最小值之差的绝对值,则随机变量
为与桌面接触的3个面上的3个数字中最大值与最小值之差的绝对值,则随机变量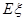 等于 。
等于 。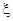 的概率分布率由下图给出:
的概率分布率由下图给出:
 ,则E
,则E


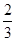 ,乙获胜的概率为
,乙获胜的概率为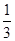 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求: