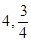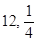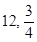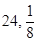题目内容
甲乙两人进行象棋比赛,规定:每次胜者得1分,负者得0分;当其中一人的得分比另一人的得分多2分时则赢得这场比赛,此时比赛结束;同时规定比赛的次数最多不超过6次,即经6次比赛,得分多者赢得比赛,得分相等为和局。已知每次比赛甲获胜的概率为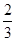 ,乙获胜的概率为
,乙获胜的概率为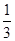 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求:
(1)ξ=2的概率;
(2)随机变量ξ的分布列及数学期望。
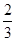 ,乙获胜的概率为
,乙获胜的概率为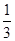 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求:(1)ξ=2的概率;
(2)随机变量ξ的分布列及数学期望。
(Ⅰ)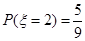 (Ⅱ)
(Ⅱ)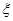 的分布列为:
的分布列为:
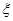 的数学期望为:
的数学期望为:
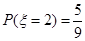 (Ⅱ)
(Ⅱ)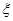 的分布列为:
的分布列为: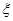 | 2 | 4 | 6 |
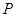 | 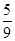 | 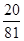 | 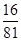 |
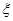 的数学期望为:
的数学期望为:
本试题主要是考查了对立事件,独立事件的概率的公式的运用,以及分布列的求解
求解和期望值的运算的综合运用。
(1)利用已知条件明白事件间的关系式,然后借助于对立事件的概率公式解得
(2)先分析随机变量的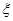 的可能取值为:2、4、6,然后利用独立事件的概率的乘法公式和互斥时间 的概率的加法公式得到分布列和期望值。
的可能取值为:2、4、6,然后利用独立事件的概率的乘法公式和互斥时间 的概率的加法公式得到分布列和期望值。
解:记“甲在第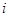 次获胜”为事件
次获胜”为事件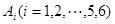
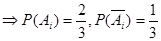
(Ⅰ)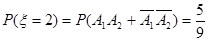 ……4分
……4分
(Ⅱ)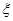 的可能取值为:2、4、6,则:由(Ⅰ)知:
的可能取值为:2、4、6,则:由(Ⅰ)知: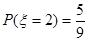
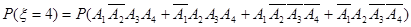
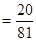
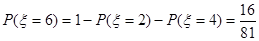 ,则
,则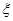 的分布列为:……9分
的分布列为:……9分
因此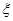 的数学期望为:
的数学期望为:
求解和期望值的运算的综合运用。
(1)利用已知条件明白事件间的关系式,然后借助于对立事件的概率公式解得
(2)先分析随机变量的
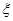 的可能取值为:2、4、6,然后利用独立事件的概率的乘法公式和互斥时间 的概率的加法公式得到分布列和期望值。
的可能取值为:2、4、6,然后利用独立事件的概率的乘法公式和互斥时间 的概率的加法公式得到分布列和期望值。解:记“甲在第
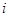 次获胜”为事件
次获胜”为事件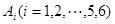
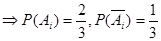
(Ⅰ)
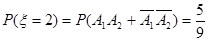 ……4分
……4分(Ⅱ)
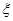 的可能取值为:2、4、6,则:由(Ⅰ)知:
的可能取值为:2、4、6,则:由(Ⅰ)知: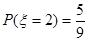
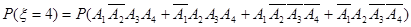
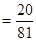
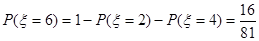 ,则
,则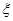 的分布列为:……9分
的分布列为:……9分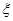 | 2 | 4 | 6 |
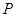 | 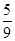 | 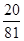 | 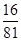 |
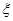 的数学期望为:
的数学期望为:

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是  ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下: 对
对


 对
对


 对
对
 .
. ,
, .
. (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是 .
.  时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求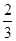 和
和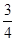 ,且各株大树是否成活互不影响.
,且各株大树是否成活互不影响. ,求
,求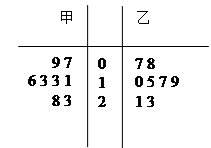
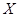 的分布列和均值.(8分)
的分布列和均值.(8分)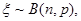 已知
已知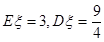 ,则
,则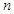 与
与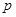 值分别为( )
值分别为( )