题目内容
(本小题满分12分)
NBA总决赛采用“7场4胜制”,由于NBA有特殊的政策和规则,能进入决赛的球队实力都较强,因此可以认为,两个队在每一场比赛中取胜的概率相等。根据不完全统计,主办一场决赛,每一方组织者有望通过出售电视转播权、门票及零售商品、停车费、广告费等收入获取收益2000万美元(1)求比赛场数 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
NBA总决赛采用“7场4胜制”,由于NBA有特殊的政策和规则,能进入决赛的球队实力都较强,因此可以认为,两个队在每一场比赛中取胜的概率相等。根据不完全统计,主办一场决赛,每一方组织者有望通过出售电视转播权、门票及零售商品、停车费、广告费等收入获取收益2000万美元(1)求比赛场数
 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。(1) 的分布列为:
的分布列为:
(2)组织者收益的数学期望11625万美元。
 的分布列为:
的分布列为:  | 4 | 5 | 6 | 7 |
| P |  |  |  |  |
本题考查离散型随机变量的分布列和期望,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,但是要注意解题格式.
(1)所需比赛场数X是随机变量,其所有可能取值为4,5,6,7,根据两个队在每一场比赛中取胜的概率相等,得到变量 符合独立重复试验,根据独立重复试验的概率公式写出分布列.
(2)根据上一问做出的X的分布列,写出期望的表示式,做出结果,根据一场收入获取收益2 000万美元,得到组织者收益的数学期望.
解:比赛场数 是随机变量,其可取值为4、5、6、7,即
是随机变量,其可取值为4、5、6、7,即 ,
, =4、5、6、7,
=4、5、6、7,
-------------------1分
依题意知:最终获胜队在第 场比赛获胜后结束比赛,必在前面
场比赛获胜后结束比赛,必在前面 —1场中获胜3场,从而,
—1场中获胜3场,从而, =
=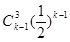 ,
, =4、5、6、7, --------------------5分
=4、5、6、7, --------------------5分
(1) 的分布列为:
的分布列为:
-------------------9分
(2)所需比赛场数的数学期望为 ,
,
故组织者收益的数学期望为 2000=11625万美元------------------11分
2000=11625万美元------------------11分
答:组织者收益的数学期望11625万美元。 -----------------12分
(1)所需比赛场数X是随机变量,其所有可能取值为4,5,6,7,根据两个队在每一场比赛中取胜的概率相等,得到变量 符合独立重复试验,根据独立重复试验的概率公式写出分布列.
(2)根据上一问做出的X的分布列,写出期望的表示式,做出结果,根据一场收入获取收益2 000万美元,得到组织者收益的数学期望.
解:比赛场数
 是随机变量,其可取值为4、5、6、7,即
是随机变量,其可取值为4、5、6、7,即 ,
, =4、5、6、7,
=4、5、6、7,-------------------1分
依题意知:最终获胜队在第
 场比赛获胜后结束比赛,必在前面
场比赛获胜后结束比赛,必在前面 —1场中获胜3场,从而,
—1场中获胜3场,从而, =
=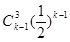 ,
, =4、5、6、7, --------------------5分
=4、5、6、7, --------------------5分(1)
 的分布列为:
的分布列为:  | 4 | 5 | 6 | 7 |
| P |  |  |  |  |
(2)所需比赛场数的数学期望为
 ,
,故组织者收益的数学期望为
 2000=11625万美元------------------11分
2000=11625万美元------------------11分答:组织者收益的数学期望11625万美元。 -----------------12分

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
 为选取女生的人数,求
为选取女生的人数,求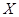 表示所有被取球的编号之和.
表示所有被取球的编号之和.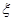 的分布列如下:
的分布列如下: ,则y的值为 .
,则y的值为 .
 三个社区中各选一人,求恰好有2人是低碳族的概率;
三个社区中各选一人,求恰好有2人是低碳族的概率; 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是  ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下: 对
对


 对
对


 对
对
 .
. ,
, .
. ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 表示取到次品的个数,则E
表示取到次品的个数,则E 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为 ,展开式的所有二项式
,展开式的所有二项式 ,若
,若 ,则
,则