题目内容
一组数据的平均数是2,方差是3,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是_______和_________.
62,3
试题分析:设这组数据分别为x1,x2,…,xn,则
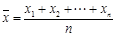 ,方差为
,方差为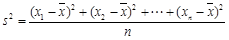 ,每一组数据都加60后,
,每一组数据都加60后,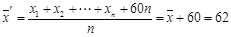 ,方差
,方差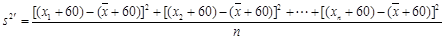
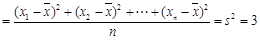
点评:若在原来数据前乘以同一个数,平均数也乘以同一个数,而方差要乘以这个数的平方,在数据上同加或减同一个数,方差不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
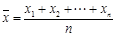 ,方差为
,方差为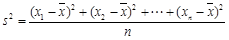 ,每一组数据都加60后,
,每一组数据都加60后,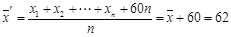 ,方差
,方差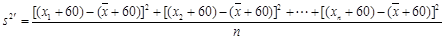
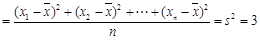

 阅读快车系列答案
阅读快车系列答案