题目内容
.(满分12分)某射击比赛,开始时在距目标100米处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150米处,这时命中记2分,且停止射击;若第二次仍未命中还可以进行第三次射击,但此时目标已在200米处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分。已知射手在100米处击中目标的概率为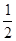 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
(1)求这名射手在射击比赛中命中目标的概率;
(2)求这名射手在比赛中得分的数学期望。
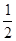 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。(1)求这名射手在射击比赛中命中目标的概率;
(2)求这名射手在比赛中得分的数学期望。
(1)为1-P(D)= 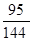
(2)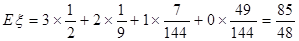
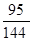
(2)
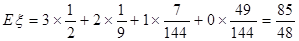
本试题主要是考查了概率的运用。古典概型概率的计算,以及相互独立事件概率的乘法公式的综合运用,以及数学的分布列和期望值的求解问题。
(1)由于记“第一、二、三次射击命中目标”分别为事件A,B,C,“三次都未击中”为事件D,则P(A)=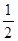 设在x米处击中概率为P(x)则P(x)=
设在x米处击中概率为P(x)则P(x)=  ,根据因为 x=100时P(A)=
,根据因为 x=100时P(A)= 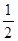 所以k=5000,得到解析式。从而得到各个事件的概率值,
所以k=5000,得到解析式。从而得到各个事件的概率值,
(2)根据上一问中概率值,可知随机变量取值的各个概率值,然后得到分布列和数学期望值。
记“第一、二、三次射击命中目标”分别为事件A,B,C,“三次都未击中”为事件D,
则P(A)=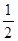 设在x米处击中概率为P(x)则P(x)=
设在x米处击中概率为P(x)则P(x)= 
因为 x=100时P(A)=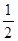 所以k=5000, P(x)=
所以k=5000, P(x)= 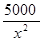
P(B)=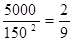 P(C)=
P(C)=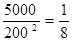 P(D)=
P(D)= 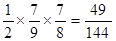
(1)为1-P(D)=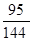
(2)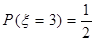
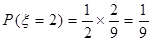
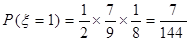
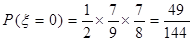
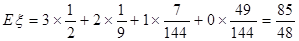
(1)由于记“第一、二、三次射击命中目标”分别为事件A,B,C,“三次都未击中”为事件D,则P(A)=
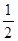 设在x米处击中概率为P(x)则P(x)=
设在x米处击中概率为P(x)则P(x)=  ,根据因为 x=100时P(A)=
,根据因为 x=100时P(A)= 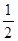 所以k=5000,得到解析式。从而得到各个事件的概率值,
所以k=5000,得到解析式。从而得到各个事件的概率值,(2)根据上一问中概率值,可知随机变量取值的各个概率值,然后得到分布列和数学期望值。
记“第一、二、三次射击命中目标”分别为事件A,B,C,“三次都未击中”为事件D,
则P(A)=
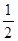 设在x米处击中概率为P(x)则P(x)=
设在x米处击中概率为P(x)则P(x)= 
因为 x=100时P(A)=
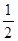 所以k=5000, P(x)=
所以k=5000, P(x)= 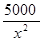
P(B)=
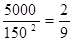 P(C)=
P(C)=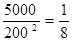 P(D)=
P(D)= 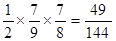
(1)为1-P(D)=
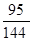
(2)
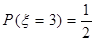
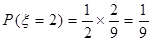
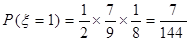
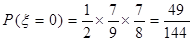
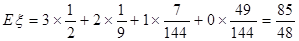

练习册系列答案
相关题目
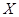 表示所有被取球的编号之和.
表示所有被取球的编号之和. 两个代表队进行乒乓球对抗赛,每队三名队员,
两个代表队进行乒乓球对抗赛,每队三名队员, 队队员是
队队员是  ,
, 队队员是
队队员是 ,按以往多次比赛的统计,对阵队员之间的胜负概率如下:
,按以往多次比赛的统计,对阵队员之间的胜负概率如下: 对
对


 对
对


 对
对
 .
. ,
, .
.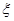 ~
~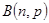 ,且
,且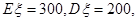 则
则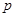 等于 ( )
等于 ( ) 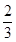
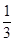
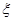 为与桌面接触的4个面上数字中偶数的个数,求
为与桌面接触的4个面上数字中偶数的个数,求 (
( )个大小相同的球,其中有3个红球和
)个大小相同的球,其中有3个红球和 个白球.已知从口袋中随机取出一个球是红球的概率是
个白球.已知从口袋中随机取出一个球是红球的概率是 .
.  时,不放回地从口袋中随机取出3个球,求取到白球的个数
时,不放回地从口袋中随机取出3个球,求取到白球的个数 的期望
的期望 ;
; ,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于 ,求
,求 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 ,求
,求 的展开式的所有项的系数的和为
的展开式的所有项的系数的和为 ,展开式的所有二项式
,展开式的所有二项式 ,若
,若 ,则
,则