题目内容
【题目】已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为![]() ,这两条曲线在第一象限的交点为
,这两条曲线在第一象限的交点为![]() ,
, ![]() 是以
是以![]() 为底边的等腰三角形.若
为底边的等腰三角形.若![]() ,记椭圆与双曲线的离心率分别为
,记椭圆与双曲线的离心率分别为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】设椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,(m>n),
由于△PF1F2是以PF1为底边的等腰三角形。若|PF1|=10,
即有m=10,n=2c,
由椭圆的定义可得m+n=2a1,
由双曲线的定义可得mn=2a2,
即有a1=5+c,a2=5c,(c<5),
再由三角形的两边之和大于第三边,可得2c+2c>10,
可得c>![]() ,即有
,即有![]() 由离心率公式可得
由离心率公式可得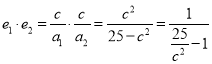
由于![]() ,则有
,则有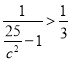 .
.
则![]() 的取值范围为(
的取值范围为(![]() ,+∞).
,+∞).
故选:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目