题目内容
【题目】已知命题p:方程 ![]() 表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
表示焦点在y轴上的椭圆,命题q:关于x的方程x2+2mx+2m+3=0无实根,若“p∧q”为假命题,“p∨q”为真命题,求实数m的取值范围.
【答案】解:∵方程 ![]() 表示焦点在y轴上的椭圆, ∴0<m+1<3﹣m,
表示焦点在y轴上的椭圆, ∴0<m+1<3﹣m,
解得:﹣1<m<1,
∴若命题p为真命题,求实数m的取值范围是(﹣1,1);
若关于x的方程x2+2mx+2m+3=0无实根,则判别式△=4m2﹣4(2m+3)<0,
即m2﹣2m﹣3<0,得﹣1<m<3.
若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,
若p真q假,则 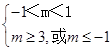 ,此时无解,
,此时无解,
柔p假q真,则 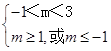 ,得1≤m<3.
,得1≤m<3.
综上,实数m的取值范围是[1,3)
【解析】若“p∧q”为假命题,“p∨q”为真命题,则p,q为一个真命题,一个假命题,进而可得实数m的取值范围.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
