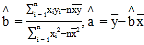Question

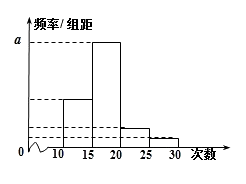
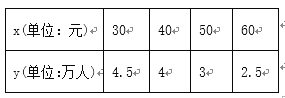
【题目】如图，矩形ABCD中，AB=2AD，E为边AB的中点，将△ADE沿直线DE翻转成△A1DE（A1平面ABCD），若M、O分别为线段A1C、DE的中点，则在△ADE翻转过程中，下列说法错误的是（ ）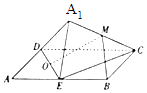
A.与平面A1DE垂直的直线必与直线BM垂直
B.异面直线BM与A1E所成角是定值
C.一定存在某个位置，使DE⊥MO
D.三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值

Answer 1

【答案】C
【解析】解：对于A，延长CB，DE交于H，连接A1H，由E为AB的中点，

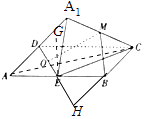
可得B为CH的中点，又M为A1C的中点，可得BM∥A1H，BM平面A1DE，

A1H平面A1DE，则BM∥平面A1DE，故与平面A1DE垂直的直线必与直线BM垂直，则A正确；

对于B，设AB=2AD=2a，过E作EG∥BM，G∈平面A1DC，

则∠A1EG=∠EA1H，

在△EA1H中，EA1=a，EH=DE= a，A1H= = ，则∠EA1H为定值，即∠A1EG为定值，则B正确；

对于C，连接A1O，可得DE⊥A1O，若DE⊥MO，即有DE⊥平面A1MO，

即有DE⊥A1C，由A1C在平面ABCD中的射影为AC，

可得AC与DE垂直，但AC与DE不垂直．

则不存在某个位置，使DE⊥MO，则C不正确；

对于D，连接OA，由直角三角形斜边的中线长为斜边的一半，可得

三棱锥A1﹣ADE外接球球心为O，半径为 ，

即有三棱锥A1﹣ADE外接球半径与棱AD的长之比为定值．则D正确．

故选：C．