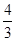题目内容
已知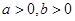 ,若直线
,若直线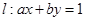 平分圆
平分圆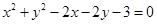 的周长,则
的周长,则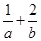 的最小值为
的最小值为
A.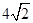 | B.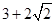 | C.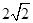 | D.1 |
B
解析试题分析:圆的方程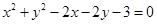 化为标准方程:
化为标准方程: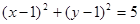 ,圆心为
,圆心为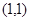 ,由题意
,由题意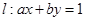 过圆心
过圆心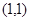 ,所以
,所以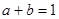 ,
,
所以 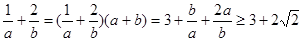
考点:直线与圆的位置关系;函数的最值.
点评:本题考查直线与圆的位置关系,以及基本不等式求最值,其中由直线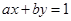 平分圆
平分圆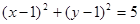 的周长得到直线过圆心是本题的突破点.同时本题根据题目条件构造出了
的周长得到直线过圆心是本题的突破点.同时本题根据题目条件构造出了
可以利用基本不等式求最值的形式,属于积定和最小型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若方程 表示的曲线为圆,则
表示的曲线为圆,则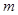 的取值范围是( )
的取值范围是( )
A. | B.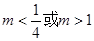 . . |
C.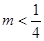 | D.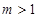 |
已知直线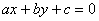 与圆
与圆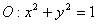 相交于
相交于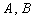 两点,且
两点,且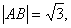 则
则 的值是
的值是
A.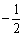 | B.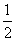 | C.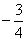 | D.0 |
直线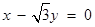 截圆
截圆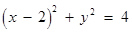 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.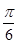 | B.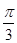 | C.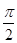 | D.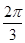 |
若点 在圆C:
在圆C:  的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |
以点(-5,4)为圆心,且与 轴相切的圆的方程是( )
轴相切的圆的方程是( )
A. | B. |
C.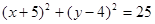 | D. |
已知点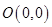 ,
,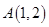 ,
,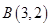 ,以线段
,以线段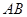 为直径作圆
为直径作圆 ,则直线
,则直线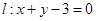 与圆
与圆 的位置关系是
的位置关系是
| A.相交且过圆心 | B.相交但不过圆心 | C.相切 | D.相离 |
已知直线 与圆
与圆 交于
交于 两点,且
两点,且 (其中
(其中 为坐标原点),则实数
为坐标原点),则实数 的值为
的值为
A. | B. | C. 或 或 | D. 或 或 |
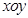 中,圆
中,圆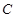 的方程为
的方程为 ,若直线
,若直线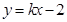 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,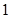 为半径的圆与圆
为半径的圆与圆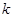 的最大值为
的最大值为