题目内容
在同一坐标系下,直线ax+by=ab和圆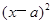 +
+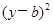 =
=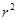 (ab≠0,r>0)的图像可能是
(ab≠0,r>0)的图像可能是
D
解析试题分析:根据题意,由于直线ax+by=ab和圆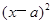 +
+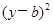 =
=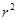 (ab≠0,r>0),圆心(a,b),半径为r,那么利用点到直线的距离公式可知为d=
(ab≠0,r>0),圆心(a,b),半径为r,那么利用点到直线的距离公式可知为d=  ,如果线与圆相离,则可知
,如果线与圆相离,则可知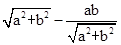 >r,对于 图象A,不成立,对于B,C圆心坐标的正负情况确定了直线的位置与圆的位置不成立,故选D.
>r,对于 图象A,不成立,对于B,C圆心坐标的正负情况确定了直线的位置与圆的位置不成立,故选D.
考点:直线与圆
点评:主要是考查了直线与圆的位置关系的运用,属于基础题。

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
若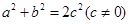 ,则直线
,则直线 被圆
被圆 所截得的弦长为 ( )
所截得的弦长为 ( )
A. | B.1 | C. | D. |
直线3x-4y-4=0被圆(x-3)2+y2=9截得的弦长为( )
A. | B.4 | C. | D. 2 |
直线 截圆x2+y2=4得的劣弧所对的圆心角是( )
截圆x2+y2=4得的劣弧所对的圆心角是( )
A. | B. | C. | D. |
过点 与圆
与圆 相交的所有直线中,被圆截得的弦最长的直线方程是( )
相交的所有直线中,被圆截得的弦最长的直线方程是( )
A. | B. | C. | D. |
若方程 表示的曲线为圆,则
表示的曲线为圆,则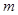 的取值范围是( )
的取值范围是( )
A. | B.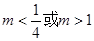 . . |
C.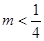 | D.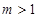 |
设直线 与圆
与圆 相交于
相交于 点,则弦
点,则弦 的长等于( )
的长等于( )
A. | B. | C.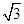 | D.1 |
圆C1 :(x+1)2+(y+4)2=16与圆C2 : (x-2)2+(y+2)2=9的位置关系是( ).
| A.相交 | B.外切 | C.内切 | D.相离 |
若点 在圆C:
在圆C:  的外部,则直线
的外部,则直线 与圆C的位置关系是( )
与圆C的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.相交或相切 |