题目内容
(12分)
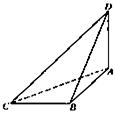
已知斜三棱柱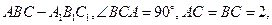
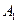 在底面
在底面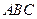 上的射影恰为
上的射影恰为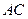 的中点
的中点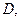 又知
又知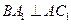 ;
;

(1)求证 :
: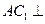 平面
平面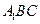 ;
;
(2)求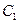 到平面
到平面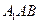 的距离;
的距离;
(3)求二面角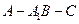 的余弦值;
的余弦值;
已知斜三棱柱
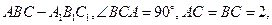
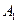 在底面
在底面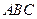 上的射影恰为
上的射影恰为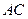 的中点
的中点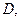 又知
又知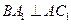 ;
;
(1)求证
 :
: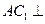 平面
平面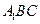 ;
;(2)求
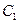 到平面
到平面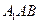 的距离;
的距离;(3)求二面角
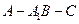 的余弦值;
的余弦值;(1)略
(2)略
(3)
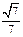
(1)∵A1在底面ABC上的射影为AC的中点D
∴平面A1ACC1⊥平面ABC∵BC⊥AC且平面A1ACC1∩平面ABC="AC "
∴BC⊥平面A1ACC1 ∴BC⊥AC1
∵AC1⊥BA1且BC∩BA1="B " ∴AC1⊥平面A1BC ----------4分
(2)如图所示,以C为坐标原点建立空间直角坐标系

∵AC1⊥平面A1BC ∴AC1⊥A1C
∴四边形A1ACC1是菱形 ∵D是AC中点
∴∠A1AD=60°∴A(2,0,0) A1(1,0,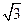 ) B(0,2,0)
) B(0,2,0)
C1(-1,0,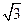 ) ∴
) ∴ =(1,0,
=(1,0,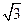
 )
) 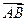 =(-2,2,0)
=(-2,2,0)
设平面A1AB的法向量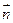 ="(x,y,z) " ∴
="(x,y,z) " ∴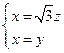 令z="1 " ∴
令z="1 " ∴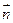 =(
=(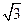 ,
,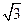 ,1)
,1)
∵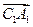 ="(2,0,0) " ∴
="(2,0,0) " ∴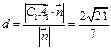 ∴C1到平面A1
∴C1到平面A1 AB的距离是
AB的距离是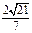 --8分
--8分
(3)平面A1AB的法向量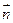 =(
=(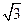 ,
,
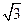 ,1)
,1)  平面A1BC的法向量
平面A1BC的法向量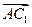 =(-3,0,
=(-3,0,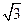 )
)
∴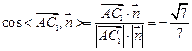 设二面角A-A1B-C的平面角为
设二面角A-A1B-C的平面角为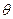 ,
,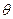 为锐角,
为锐角,
∴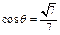 ∴二面角
∴二面角 A-A1B-C的余弦值为
A-A1B-C的余弦值为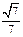 -------------
------------- --12分
--12分
∴平面A1ACC1⊥平面ABC∵BC⊥AC且平面A1ACC1∩平面ABC="AC "
∴BC⊥平面A1ACC1 ∴BC⊥AC1
∵AC1⊥BA1且BC∩BA1="B " ∴AC1⊥平面A1BC ----------4分
(2)如图所示,以C为坐标原点建立空间直角坐标系

∵AC1⊥平面A1BC ∴AC1⊥A1C
∴四边形A1ACC1是菱形 ∵D是AC中点
∴∠A1AD=60°∴A(2,0,0) A1(1,0,
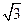 ) B(0,2,0)
) B(0,2,0)C1(-1,0,
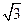 ) ∴
) ∴ =(1,0,
=(1,0,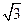
 )
) 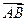 =(-2,2,0)
=(-2,2,0)设平面A1AB的法向量
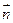 ="(x,y,z) " ∴
="(x,y,z) " ∴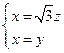 令z="1 " ∴
令z="1 " ∴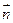 =(
=(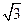 ,
,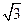 ,1)
,1)∵
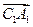 ="(2,0,0) " ∴
="(2,0,0) " ∴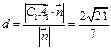 ∴C1到平面A1
∴C1到平面A1 AB的距离是
AB的距离是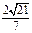 --8分
--8分(3)平面A1AB的法向量
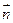 =(
=(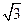 ,
,
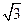 ,1)
,1)  平面A1BC的法向量
平面A1BC的法向量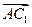 =(-3,0,
=(-3,0,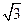 )
)∴
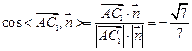 设二面角A-A1B-C的平面角为
设二面角A-A1B-C的平面角为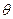 ,
,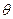 为锐角,
为锐角,∴
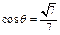 ∴二面角
∴二面角 A-A1B-C的余弦值为
A-A1B-C的余弦值为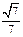 -------------
------------- --12分
--12分
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目


 的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA
的菱形,∠ACC1为锐角,侧面ABB1A1⊥侧面AA 1C1C,且A1B=AB=AC=1.
1C1C,且A1B=AB=AC=1.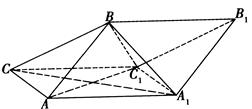
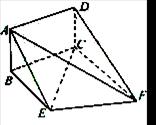
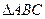 是腰长为2的等腰直角三角形(如图1),
是腰长为2的等腰直角三角形(如图1), ,在边
,在边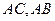 上分别取点
上分别取点 ,使得
,使得 ,把
,把 沿直线
沿直线 折起,使
折起,使 =90°,得四棱锥
=90°,得四棱锥 (如图2).在四棱锥
(如图2).在四棱锥
 (I)求证:CE⊥AF;
(I)求证:CE⊥AF;  时,试在
时,试在 上确定一点G,使得
上确定一点G,使得 ,并证明你的结论.
,并证明你的结论.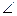 BCF=
BCF=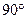 ,AD=
,AD=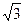 ,EF=2.
,EF=2.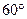 .
.
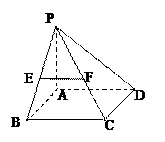
 的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC
的棱AP、AB上的点,且AD:DP=AE:EB=1:3.求证:DE//平面PBC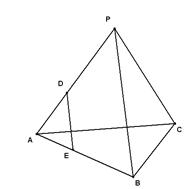
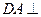 平面ABC,
平面ABC,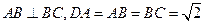 ,则球O的体积等于 。
,则球O的体积等于 。