题目内容
(本小题满分12分)
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,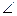 BCF=
BCF=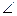 CEF=
CEF=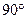 ,AD=
,AD=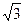 ,EF=2.
,EF=2.
(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为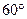 .
.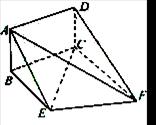
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,
 BCF=
BCF= CEF=
CEF=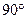 ,AD=
,AD=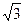 ,EF=2.
,EF=2.(1)求证:AE//平面DCF;
(2)当AB的长为何值时,二面角A-EF-C的大小为
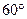 .
.
(1) 略
(2)

方法一:(Ⅰ)证明:过点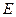 作
作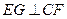 交
交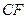 于
于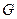 ,连结
,连结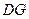 ,
,
可得四边形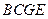 为矩形,又
为矩形,又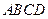 为矩形,所以
为矩形,所以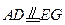 ,
,
从而四边形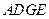 为平行四边形,故
为平行四边形,故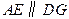 .因为
.因为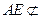 平面
平面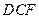 ,
,

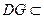 平面
平面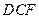 ,
,
所以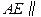 平面
平面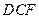 .………6分
.………6分
(Ⅱ)解:过点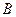 作
作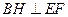 交
交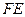 的延长线于
的延长线于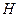 ,连结
,连结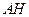 .
.
由平面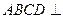 平面
平面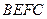 ,
,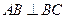 ,得
,得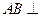 平面
平面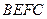 ,
,
从而 .所以
.所以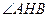 为二面角
为二面角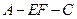 的平面角.
的平面角.
在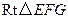 中,因为
中,因为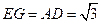 ,
,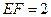 ,
,
所以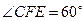 ,
,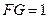 .又因为
.又因为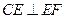 ,所以
,所以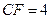 ,
,
从而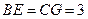 ,于是
,于是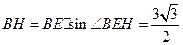 ,因为
,因为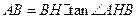 所以当
所以当 为
为 时,二面角
时,二面角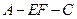 的大小为
的大小为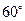 ………12分
………12分
方法二:如图,以点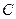 为坐标原点,以
为坐标原点,以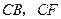 和
和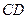 分别作为
分别作为 轴,
轴,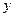 轴和
轴和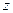 轴,建立空间直角坐标系
轴,建立空间直角坐标系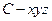 .设
.设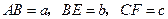 ,
,
则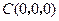 ,
,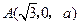 ,
,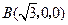 ,
,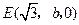 ,
,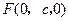 .
.
(Ⅰ)证明: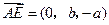 ,
,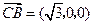 ,
,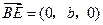 ,
,
所以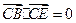 ,
,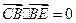 ,从而
,从而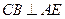 ,
,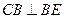 ,
,
所以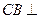 平面
平面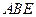 .因为
.因为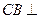 平面
平面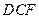 ,所以平面
,所以平面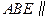 平面
平面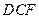 .
.
故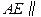 平面
平面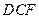 .………6分
.………6分
(Ⅱ)解:因为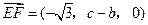 ,
, ,所以
,所以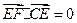 ,
,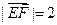 ,从而
,从而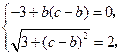
解得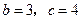 .所以
.所以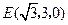 ,
,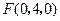 .设
.设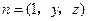 与平面
与平面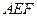 垂直,
垂直,
则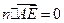 ,
,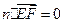 ,解得
,解得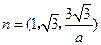 .又因为
.又因为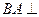 平面
平面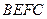 ,
, ,所以
,所以 ,
,
得到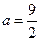 .所以当
.所以当 为
为 时,二面角
时,二面角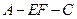 的大小为
的大小为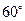 .………12分
.………12分
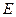 作
作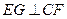 交
交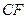 于
于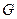 ,连结
,连结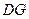 ,
,可得四边形
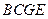 为矩形,又
为矩形,又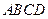 为矩形,所以
为矩形,所以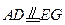 ,
,从而四边形
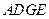 为平行四边形,故
为平行四边形,故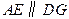 .因为
.因为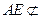 平面
平面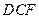 ,
,
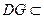 平面
平面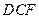 ,
,所以
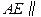 平面
平面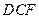 .………6分
.………6分(Ⅱ)解:过点
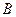 作
作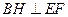 交
交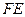 的延长线于
的延长线于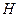 ,连结
,连结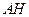 .
.由平面
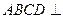 平面
平面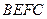 ,
,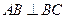 ,得
,得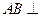 平面
平面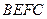 ,
,从而
 .所以
.所以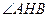 为二面角
为二面角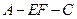 的平面角.
的平面角.在
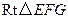 中,因为
中,因为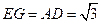 ,
,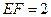 ,
,所以
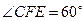 ,
,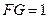 .又因为
.又因为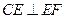 ,所以
,所以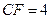 ,
,从而
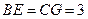 ,于是
,于是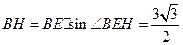 ,因为
,因为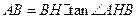 所以当
所以当 为
为 时,二面角
时,二面角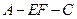 的大小为
的大小为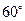 ………12分
………12分方法二:如图,以点
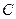 为坐标原点,以
为坐标原点,以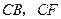 和
和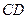 分别作为
分别作为 轴,
轴,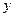 轴和
轴和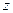 轴,建立空间直角坐标系
轴,建立空间直角坐标系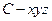 .设
.设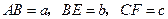 ,
,则
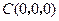 ,
,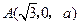 ,
,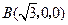 ,
,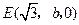 ,
,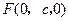 .
.(Ⅰ)证明:
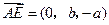 ,
,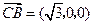 ,
,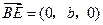 ,
,所以
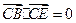 ,
,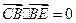 ,从而
,从而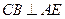 ,
,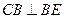 ,
,所以
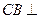 平面
平面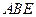 .因为
.因为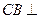 平面
平面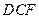 ,所以平面
,所以平面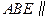 平面
平面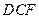 .
.故
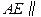 平面
平面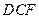 .………6分
.………6分(Ⅱ)解:因为
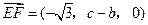 ,
, ,所以
,所以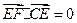 ,
,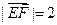 ,从而
,从而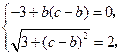
解得
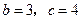 .所以
.所以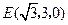 ,
,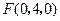 .设
.设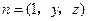 与平面
与平面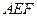 垂直,
垂直,则
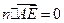 ,
,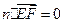 ,解得
,解得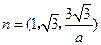 .又因为
.又因为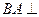 平面
平面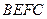 ,
, ,所以
,所以 ,
,得到
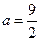 .所以当
.所以当 为
为 时,二面角
时,二面角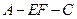 的大小为
的大小为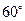 .………12分
.………12分
练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
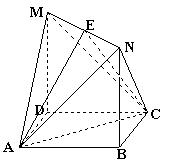
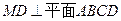 ,
, 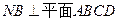 ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由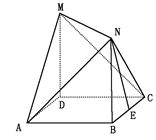
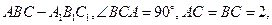
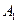 在底面
在底面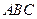 上的射影恰为
上的射影恰为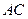 的中点
的中点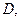 又知
又知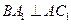 ;
;
 :
: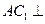 平面
平面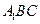 ;
;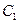 到平面
到平面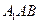 的距离;
的距离;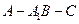 的余弦值;
的余弦值; ,CD=1.
,CD=1.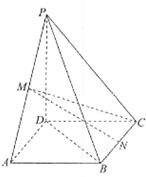
 ⊥平面AMN; (6分)
⊥平面AMN; (6分)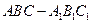 中,
中,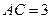 ,
,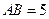 ,
,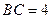 ,点
,点 是
是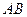 的中点,
的中点, ;
;  .
.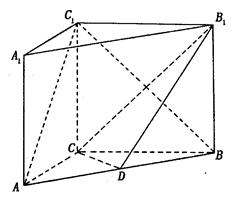
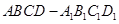 中,既与
中,既与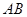 共面也与
共面也与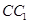 共面的棱的条数为 ( )
共面的棱的条数为 ( )