题目内容
【题目】已知数列{an}的前n项和为Sn ， 且Sn=n（n+1），
（1）求数列{an}的通项公式an
（2）数列{bn}的通项公式bn= 
，求数列{bn}的前n项和为Tn ．
【答案】
（1）解：n=1时，S1=a1=2，
n≥2时，an=Sn﹣Sn﹣1=n（n+1）﹣（n﹣1）n=2n
经检验n=1时成立，
综上 an=2n
（2）解：由（1）可知 
Tn=b1+b2+b3+…+bn
= 
= 
= 
【解析】（1）当n≥2时，由an=Sn﹣Sn﹣1=2n，再求得n=1时a1的值，检验是否满足n≥2时的关系式，从而可得数列{an}的通项公式an；（2）利用裂项法可得bn= 
（ 
﹣ 
），从而可得数列{bn}的前n项和为Tn ．
【考点精析】通过灵活运用数列的前n项和，掌握数列{an}的前n项和sn与通项an的关系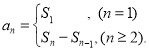
即可以解答此题．
练习册系列答案
相关题目
