题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,分别求函数
时,分别求函数![]() 的最小值和
的最小值和![]() 的最大值,并证明当
的最大值,并证明当![]() 时,
时, ![]() 成立;
成立;
(3)令![]() ,当
,当![]() 时,判断函数
时,判断函数![]() 有几个不同的零点并证明.
有几个不同的零点并证明.
【答案】(1)![]() ;(2)见解析;(3)1个
;(2)见解析;(3)1个
【解析】试题分析:(1)由题意得![]() 在
在![]() 上恒成立,根据恒成立问题的解答方法求解;
上恒成立,根据恒成立问题的解答方法求解;
(2)分别求出函数![]() 和
和![]() 的导数,研究出函数的单调性即可求出最值;
的导数,研究出函数的单调性即可求出最值;
根据题意得![]() ,可判断出
,可判断出![]() ,即
,即![]() 在
在![]() 上单调递减,得出函数至多有一个零点,再利用零点存在性定理进行判断.
上单调递减,得出函数至多有一个零点,再利用零点存在性定理进行判断.
试题解析:
(1)由题意得![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,有
,有 即
即![]() ,
,
得 ,所以
,所以![]() .
.
(2)由题意可得![]()
令![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 取最小值3,
取最小值3, ![]() ,令
,令![]() ,得
,得![]() ,
,
当![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
因为当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() .
.
(3)因为![]() ,
,
所以![]() ,
,
其定义域为![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
因为![]() ,所以
,所以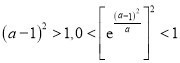 ,所以
,所以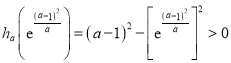 ,又
,又![]() ,所以函数
,所以函数![]() 只有1个零点.
只有1个零点.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.

