题目内容
【题目】已知![]() 分别是椭圆
分别是椭圆![]() 的长轴与短轴的一个端点,
的长轴与短轴的一个端点, ![]() 是椭圆的左、右焦点,以
是椭圆的左、右焦点,以![]() 点为圆心、3为半径的圆与以
点为圆心、3为半径的圆与以![]() 点为圆心、1为半径的圆的交点在椭圆
点为圆心、1为半径的圆的交点在椭圆![]() 上,且
上,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求证:
,求证: ![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:根据题意列方程,利用待定系数法解方程求出椭圆的标准方程,第二步设出点P的坐标,满足椭圆方程作为条件(1),写出直线AP、BP的方程,表示点M、N的坐标,得到![]() 和
和![]() 的长的表达式,两者相乘,代入条件(1)并化简所得的积,化简后恰好为
的长的表达式,两者相乘,代入条件(1)并化简所得的积,化简后恰好为![]() .
.
试题解析:
(1)由题意得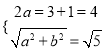 ,解得
,解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)及题意可画图,如图,不妨令![]() .设
.设![]() ,则
,则![]() .
.
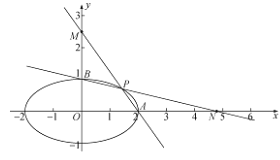
令![]() ,得
,得![]() ,从而
,从而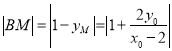 ;直线
;直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,从而
,从而 .
.
所以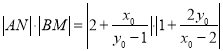
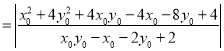
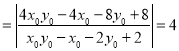 .
.
当![]() 时,
时, ![]() ,
,
所以![]() ,综上可知
,综上可知![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目