题目内容
【题目】如图,设抛物线C1:y2=4mx(m>0)的准线与x轴交于F1 , 焦点为F2;以F1 , F2为焦点,离心率e=![]() 的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
的椭圆C2与抛物线C1在x轴上方的交点为P,延长PF2交抛物线于点Q,M是抛物线C1上一动点,且M在P与Q之间运动.
当m=1时,求椭圆C2的方程;
【答案】解:当m=1时,y2=4x,则F1(﹣1,0),F2(1,0)
设椭圆方程为![]() =1(a>b>0),则c=1,又e=
=1(a>b>0),则c=1,又e=![]() =
=![]() ,所以a=2,b2=3
,所以a=2,b2=3
所以椭圆C2方程为![]() =1
=1
【解析】当m=1时,y2=4x,则F1(﹣1,0),F2(1,0).设椭圆方程为![]() (a>b>0),由题设条件知c=1,a=2,b2=3,由此可知椭圆C2方程为
(a>b>0),由题设条件知c=1,a=2,b2=3,由此可知椭圆C2方程为![]()
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1))和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.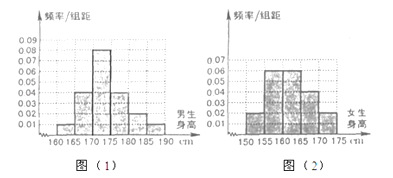
(Ⅰ)试问在抽取的学生中,男、女生各有多少人?
(Ⅱ)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
≥170cm | <170cm | 总计 | |
男生身高 | |||
女生身高 | |||
总计 |
(Ⅲ)在上述80名学生中,从身高在170~175cm之间的学生中按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式:K2=![]()
参考数据:
P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 5.024 | 6.635 | 7.879 | 10.828 |