题目内容
9．已知数列{an}满足a1=3，an+1=$\frac{1}{2}$an+1（n∈N*），则an=2+$\frac{1}{{2}^{n-1}}$．分析 通过对an+1=$\frac{1}{2}$an+1（n∈N*）变形可知数列{an-2}是以1为首项、$\frac{1}{2}$为公比的等比数列，进而计算可得结论．
解答 解：∵an+1=$\frac{1}{2}$an+1（n∈N*），
∴an+1-2=$\frac{1}{2}$（an-2）（n∈N*），
又∵a1=3，a1-2=3-2=1，
∴an-2=1•$\frac{1}{{2}^{n-1}}$，
∴an=2+$\frac{1}{{2}^{n-1}}$，
故答案为：2+$\frac{1}{{2}^{n-1}}$．
点评 本题考查数列的通项，注意解题方法的积累，属于中档题．
练习册系列答案
优学名师名题系列答案
相关题目
17．从1，2，3，4这四个数中一次随机选取两个数，所取两个数之和为5的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
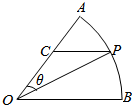如图，扇形AOB，圆心角AOB等于60°，半径为2，在弧AB上有一动点P，过P引平行于OB的直线和OA交于点C，设∠AOP=θ．
如图所示，某企业拟建造一个体积为V的圆柱型的容器（不计厚度，长度单位：米）．已知圆柱两个底面部分每平方米建造费用为a千元，侧面部分每平方米建造费用为2a千元．假设该容器的建造费用仅与其表面积有关，设圆柱的底面半径为r，该容器的总建造费用为y千元．