题目内容
17.在函数y=$\frac{\sqrt{1-x}}{x+2}$中,自变量x的取值范围是x≤1且x≠-2.分析 根据函数y的解析式,列出使解析式有意义的关于自变量x的不等式组,求出x的取值范围即可.
解答 解:∵函数y=$\frac{\sqrt{1-x}}{x+2}$,
∴$\left\{\begin{array}{l}{1-x≥0}\\{x+2≠0}\end{array}\right.$,
解得x≤1且x≠-2;
∴自变量x的取值范围是x≤1且x≠-2.
故答案为:x≤1且x≠-2.
点评 本题考查了根据函数的解析式求自变量取值范围的应用问题,是基础题目.

练习册系列答案
相关题目
9.C${\;}_{6}^{1}$+C${\;}_{6}^{2}$+C${\;}_{6}^{3}$+C${\;}_{6}^{4}$+C${\;}_{6}^{5}$的值为( )
| A. | 64 | B. | 63 | C. | 62 | D. | 61 |
6.设函数f(x)=-x2+2x+3,x∈[-5,5].若从区间内随机选取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | 0.3 | B. | 0.4 | C. | 0.5 | D. | 0.6 |
12.在△ABC中,已知$\overrightarrow{AB}•\overrightarrow{AC}$=2$\sqrt{3}$,A=60°,则△ABC的面积为( )
| A. | 1 | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
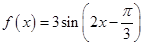 的图象为
的图象为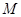 ,下列结论中正确的是( )
,下列结论中正确的是( )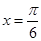 对称
对称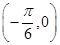 对称
对称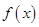 在区间
在区间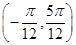 上递增
上递增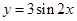 的图象向右平移
的图象向右平移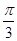 个单位长度可得
个单位长度可得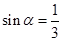 ,且
,且 为第二象限角,则
为第二象限角,则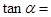 ( )
( )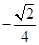 B.
B.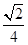 C.
C. D.
D.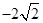
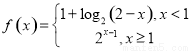 ;
;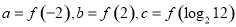 ,则( )
,则( )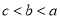 B.
B.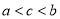
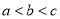 D.
D.