题目内容
1.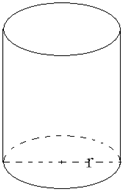 如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.
如图所示,某企业拟建造一个体积为V的圆柱型的容器(不计厚度,长度单位:米).已知圆柱两个底面部分每平方米建造费用为a千元,侧面部分每平方米建造费用为2a千元.假设该容器的建造费用仅与其表面积有关,设圆柱的底面半径为r,该容器的总建造费用为y千元.(1)写出y关于r的函数表达式;
(2)求该容器总建造费用最小时r的值.
分析 (1)设出圆柱的高,求出圆柱的高,从而求出函数表达式;
(2)先求出函数的导数,得到函数的单调区间,进而求出r的最小值.
解答 解:(1)设圆柱的高为h,
∵V=πr2h,∴$h=\frac{V}{{π\;{r^2}}}$,
∴$y=a•2π\;{r^2}+2a•2π\;rh=2aπ\;{r^2}+\frac{4aV}{r}$(r>0).
(2)$y'=4aπ\;r-\frac{4aV\;}{r^2}$,
令y′=0,得$r=\root{3}{{\frac{V}{π\;}}}$,
| r | (0,$\root{3}{{\frac{V}{π\;}}}$) | $\root{3}{{\frac{V}{π\;}}}$ | ($\root{3}{{\frac{V}{π\;}}}$Z,+∞) |
| y' | - | 0 | + |
| y | ↘ | 极小值 | ↗ |
点评 本题考查了圆柱的体积公式,考查求函数的解析式、函数的单调性、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
12.等比数列{an}的各项均为正数,且a4=4,a6=16,则公比q=( )
| A. | -4 | B. | -2 | C. | 4 | D. | 2 |
12.已知a,b为不相等的两个正数,且lgab=0,则函数y=ax和y=bx的图象之间的关系是( )
| A. | 关于原点对称 | B. | 关于y轴对称 | C. | 关于x轴对称 | D. | 关于直线y=x对称 |
12.执行如图所示的程序框图,输出的结果( )
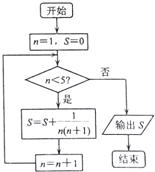

| A. | $\frac{3}{4}$ | B. | $\frac{5}{6}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{5}$ |
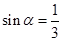 ,且
,且 为第二象限角,则
为第二象限角,则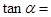 ( )
( )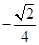 B.
B.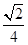 C.
C. D.
D.