题目内容
14.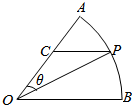 如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.
如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ.(1)若点C为OA的中点,试求θ的正弦值.
(2)求△POC面积的最大值及此时θ的值.
分析 (1)在△POC中,根据∠OCP=$\frac{2π}{3}$,OP=2,OC=1,利用余弦定理求得PC的值,由正弦定理即可求得θ的正弦值.
(2)解法一:利用正弦定理求得CP和OC的值,记△POC的面积为S(θ),则S(θ)=$\frac{1}{2}$CP•OCsin$\frac{2π}{3}$,利用两角和差的正弦公式化为 $\frac{2\sqrt{3}}{3}$(sin2θ+$\frac{π}{6}$)-$\frac{\sqrt{3}}{3}$,可得θ=$\frac{π}{6}$时,S(θ)取得最大值为$\frac{\sqrt{3}}{3}$.
解法二:利用余弦定理求得OC2+PC2+OC•PC=4,再利用基本不等式求得3OC•PC≤4,所以S=$\frac{1}{2}$CP•OCsin $\frac{2π}{3}$≤$\frac{1}{2}$×$\frac{4}{3}×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,再根据OC=PC 求得△POC面积的最大值时θ的值.
解答  解:(1)在△POC中,∠OCP=$\frac{2π}{3}$,OP=2,OC=1,
解:(1)在△POC中,∠OCP=$\frac{2π}{3}$,OP=2,OC=1,
由OP2=OC2+PC2-2OC•PCcos$\frac{2π}{3}$得PC2+PC-3=0,解得PC=$\frac{-1+\sqrt{13}}{2}$.
由正弦定理可得:sinθ$\frac{CPsin∠PCO}{OP}=\frac{(\frac{-1+\sqrt{13}}{2})×sin\frac{2π}{3}}{2}$=$\frac{\sqrt{39}-\sqrt{3}}{8}$.
(2)解法一:∵CP∥OB,∴∠CPO=∠POB=$\frac{π}{3}$-θ,
在△POC中,由正弦定理得 $\frac{OP}{sin∠PCO}=\frac{CP}{sinθ}$,
即 $\frac{2}{sin\frac{2π}{3}}=\frac{CP}{sinθ}$,∴CP=$\frac{4}{\sqrt{3}}$sinθ.
又 $\frac{OC}{sin(\frac{π}{3}-θ)}=\frac{CP}{sin\frac{2π}{3}}$,∴OC=$\frac{4}{\sqrt{3}}$sin($\frac{π}{3}$-θ).
记△POC的面积为S(θ),则S(θ)=$\frac{1}{2}$CP•OCsin$\frac{2π}{3}$=$\frac{1}{2}$•$\frac{4}{\sqrt{3}}$sinθ•$\frac{4}{\sqrt{3}}$sin($\frac{π}{3}$-θ)×$\frac{\sqrt{3}}{2}$=$\frac{4}{\sqrt{3}}$sinθ•sin($\frac{π}{3}$-θ)=$\frac{4}{\sqrt{3}}$sinθ($\frac{\sqrt{3}}{2}$cosθ-$\frac{1}{2}$sinθ)=2sinθcosθ-$\frac{2}{\sqrt{3}}$sin2θ=sin2θ+$\frac{\sqrt{3}}{3}$cos2θ-$\frac{\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$(sin2θ+$\frac{π}{6}$)-$\frac{\sqrt{3}}{3}$,
∴θ=$\frac{π}{6}$时,S(θ)取得最大值为$\frac{\sqrt{3}}{3}$.
解法二:cos$\frac{2π}{3}$=$\frac{O{C}^{2}+P{C}^{2}-4}{2OC•PC}$=-$\frac{1}{2}$,即OC2+PC2+OC•PC=4.
又OC2+PC2+OC•PC≥3OC•PC,即3OC•PC≤4,当且仅当OC=PC时等号成立,
所以S=$\frac{1}{2}$CP•OCsin $\frac{2π}{3}$≤$\frac{1}{2}$×$\frac{4}{3}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$,
∵OC=PC,
∴θ=$\frac{π}{6}$时,S(θ)取得最大值为$\frac{\sqrt{3}}{3}$.
点评 本题主要考查两角和差的正弦公式,正弦定理、余弦定理、基本不等式的应用,属于中档题.

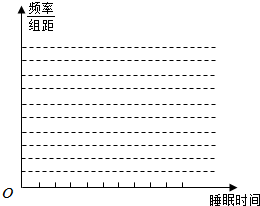 从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:
从某校高一年级随机抽取n名学生,获得了他们日平均睡眠时间(单位:小时)的数据,整理得到数据分组及频数分布表:| 组号 | 分组 | 频数 | 频率 |
| 1 | [5,6) | 2 | 0.04 |
| 2 | [6,7) | 0.20 | |
| 3 | [7,8) | a | |
| 4 | [8,9) | b | |
| 5[来源:Zxxk.Com] | [9,10) | 0.16 |
(Ⅱ)若a=10,补全表中数据,并绘制频率分布直方图;
(Ⅲ)假设同一组中的每个数据可用该组区间的中点值代替.若上述数据的平均值为7.84,求a,b的值,并由此估计该校高一学生的日平均睡眠时间不少于8小时的概率.
| A. | $\frac{π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{3}$或$\frac{2}{3}$π | D. | $\frac{5}{6}$π或$\frac{π}{6}$ |

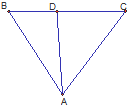 如图,已知A,B,C三点不共线.
如图,已知A,B,C三点不共线.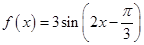 的图象为
的图象为 ,下列结论中正确的是( )
,下列结论中正确的是( ) 对称
对称 对称
对称 在区间
在区间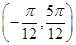 上递增
上递增 的图象向右平移
的图象向右平移 个单位长度可得
个单位长度可得