题目内容
(本题满分12分,第Ⅰ小题4分,第Ⅱ小题5分,第Ⅲ小题3分)
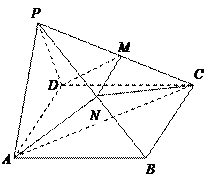
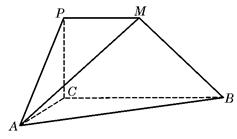 如图,
如图, 是直角梯形,∠
是直角梯形,∠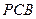 =90°,
=90°,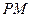 ∥
∥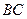 ,
,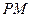 =1,
=1,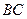 =2,又
=2,又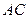 =1,∠
=1,∠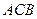 =120°,
=120°,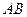 ⊥
⊥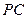 ,直线
,直线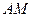 与直线
与直线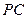 所成的角为60°.
所成的角为60°.
(Ⅰ)求证:平面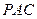 ⊥平面
⊥平面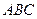 ;
;
(Ⅱ)求二面角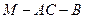 的大小;
的大小;
(Ⅲ)求三棱锥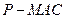 的体积.
的体积.
 如图,
如图, 是直角梯形,∠
是直角梯形,∠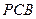 =90°,
=90°,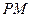 ∥
∥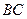 ,
,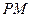 =1,
=1,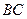 =2,又
=2,又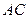 =1,∠
=1,∠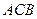 =120°,
=120°,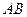 ⊥
⊥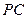 ,直线
,直线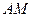 与直线
与直线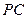 所成的角为60°.
所成的角为60°.(Ⅰ)求证:平面
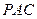 ⊥平面
⊥平面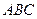 ;
;(Ⅱ)求二面角
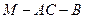 的大小;
的大小;(Ⅲ)求三棱锥
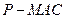 的体积.
的体积.(Ⅰ)略 (Ⅱ) 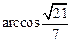 (Ⅲ)
(Ⅲ)
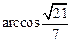 (Ⅲ)
(Ⅲ)
解法一:
(Ⅰ)∵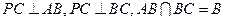
∴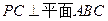 ,又∵
,又∵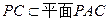 ∴
∴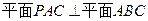 …(4分)
…(4分)
(Ⅱ)取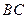 的中点
的中点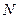 ,则
,则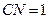 ,连结
,连结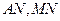 ,
,
∵ ,∴
,∴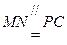 ,从而
,从而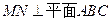
作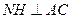 ,交
,交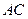 的延长线于
的延长线于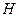 ,连结
,连结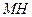 ,则由三垂线定理知,
,则由三垂线定理知,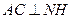 ,
,
从而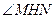 为二面角
为二面角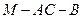 的平面角
的平面角
直线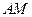 与直线
与直线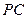 所成的角为
所成的角为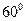 ∴
∴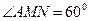
在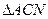 中,由余弦定理得
中,由余弦定理得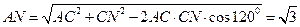
在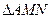 中,
中,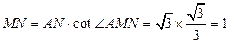
在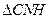 中,
中,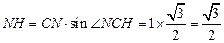
在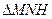 中,
中,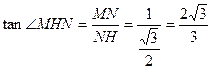
故二面角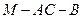 的平面角大小为
的平面角大小为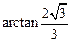 …(9分)
…(9分)
(Ⅲ)由(Ⅱ)知,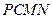 为正方形
为正方形
∴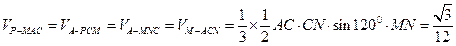 ……(12分)
……(12分)
解法二:(Ⅰ)同解法一…(4分)
(Ⅱ)在平面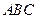 内,过
内,过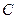 作
作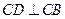 ,建立空间直角坐标系
,建立空间直角坐标系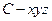 (如图)
(如图)
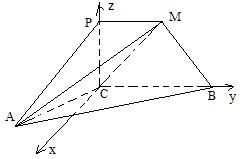 由题意有
由题意有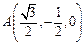 ,设
,设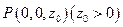 ,
,
则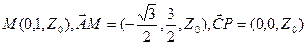
由直线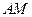 与直线
与直线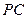 所成的解为
所成的解为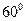 ,得
,得
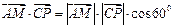 ,即
,即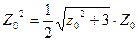 ,解得
,解得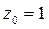
∴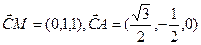 ,设平面
,设平面 的一个法向量为
的一个法向量为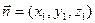 ,
,
则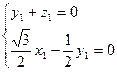 ,取
,取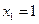 ,得
,得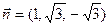
平面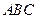 的法向量取为
的法向量取为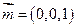 ,设
,设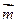 与
与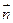 所成的角为
所成的角为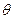 ,则
,则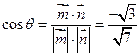
显然,二面角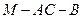 的平面角为锐角,故二面角
的平面角为锐角,故二面角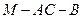 的平面角大小为
的平面角大小为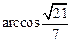
(Ⅲ)取平面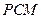 的法向量取为
的法向量取为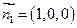 ,则点A到平面
,则点A到平面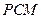 的距离
的距离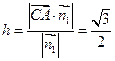
∵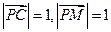 ,∴
,∴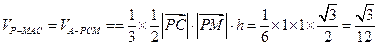 …(12分)
…(12分)
(Ⅰ)∵
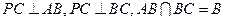
∴
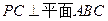 ,又∵
,又∵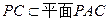 ∴
∴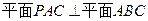 …(4分)
…(4分)(Ⅱ)取
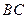 的中点
的中点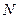 ,则
,则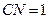 ,连结
,连结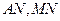 ,
,∵
 ,∴
,∴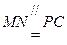 ,从而
,从而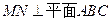
作
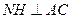 ,交
,交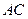 的延长线于
的延长线于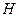 ,连结
,连结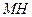 ,则由三垂线定理知,
,则由三垂线定理知,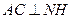 ,
,从而
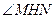 为二面角
为二面角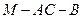 的平面角
的平面角直线
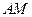 与直线
与直线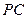 所成的角为
所成的角为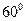 ∴
∴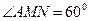
在
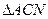 中,由余弦定理得
中,由余弦定理得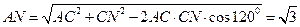
在
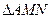 中,
中,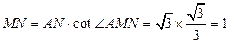
在
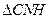 中,
中,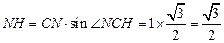
在
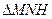 中,
中,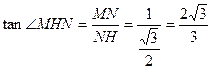
故二面角
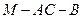 的平面角大小为
的平面角大小为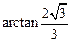 …(9分)
…(9分)(Ⅲ)由(Ⅱ)知,
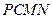 为正方形
为正方形∴
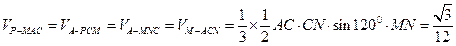 ……(12分)
……(12分)解法二:(Ⅰ)同解法一…(4分)
(Ⅱ)在平面
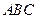 内,过
内,过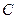 作
作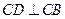 ,建立空间直角坐标系
,建立空间直角坐标系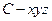 (如图)
(如图) 由题意有
由题意有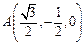 ,设
,设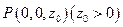 ,
,则
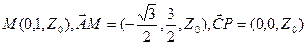
由直线
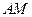 与直线
与直线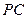 所成的解为
所成的解为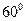 ,得
,得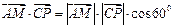 ,即
,即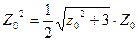 ,解得
,解得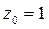
∴
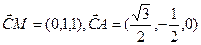 ,设平面
,设平面 的一个法向量为
的一个法向量为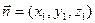 ,
,则
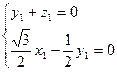 ,取
,取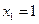 ,得
,得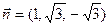
平面
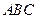 的法向量取为
的法向量取为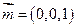 ,设
,设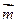 与
与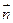 所成的角为
所成的角为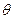 ,则
,则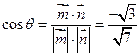
显然,二面角
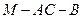 的平面角为锐角,故二面角
的平面角为锐角,故二面角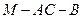 的平面角大小为
的平面角大小为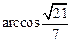
(Ⅲ)取平面
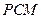 的法向量取为
的法向量取为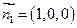 ,则点A到平面
,则点A到平面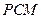 的距离
的距离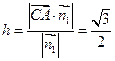
∵
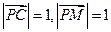 ,∴
,∴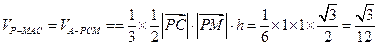 …(12分)
…(12分)
练习册系列答案
相关题目
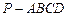 中,侧面
中,侧面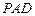
 垂直,底面
垂直,底面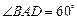 ,
,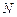 是
是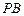 中点,过
中点,过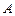 、
、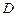 三点的平面交
三点的平面交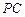 于
于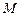 .
. 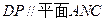 ; (2)求证:
; (2)求证: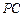 中点;(3)求证:平面
中点;(3)求证:平面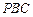 ⊥平面
⊥平面 .
.
 ,
, ,且
,且 ”的平面
”的平面 ,
,
 为其上的三个点,则在正方体盒子中,
为其上的三个点,则在正方体盒子中, ( ).
( ). 



 ⊥平面
⊥平面 ,直线
,直线
 平面
平面 ,下面有三个命题:①
,下面有三个命题:①

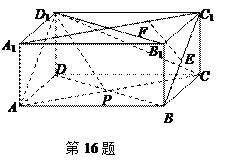
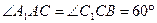 ,且平面ACC1A1⊥平面BCC1B1,则A1B的长度为 。m]
,且平面ACC1A1⊥平面BCC1B1,则A1B的长度为 。m]