题目内容
【题目】已知![]()
![]() 且
且![]()
(1)求函数![]() 的定义域及其零点;
的定义域及其零点;
(2)若关于![]() 的方程
的方程![]() 在区间[0,1)内有解,求实数
在区间[0,1)内有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)定义域为![]() ,零点为0;(2)分类讨论,答案见解析.
,零点为0;(2)分类讨论,答案见解析.
【解析】
(1)求定义域要求真数大于0,列不等式组可得结果,求零点令函数值为0,解方程可在定义域内得函数的零点;
(2)利用函数零点(方程有根)求参数范围问题,可构造新函数,转化为两个函数有交点问题,也可利用函数的单调性,确定参数的取值范围.
解:(1)由![]() 得
得![]() ,
,
故![]() 的定义域为
的定义域为![]() ,
,
由![]() ,即
,即![]() ,
,
得![]() ,
,
得![]() ,
,
解得![]() 或
或![]() ,
,
由于![]() ,故
,故![]() 的零点为0;
的零点为0;
(2)方法一:
![]() 在区间[0,1)内有解,即
在区间[0,1)内有解,即![]() ,
,![]() 有解,
有解,![]()
令![]() ,
,![]() ,
,![]() ,
,![]() 在(0,1]为减函数,
在(0,1]为减函数,
则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ;
;
方法二:
由![]() 方程在区间[0,1)内有解,即
方程在区间[0,1)内有解,即![]() 与
与![]() 在
在![]() 有交点,
有交点,
![]() .令
.令![]() ,
,![]() ,
,![]() ,
,
![]() 在(0,1]为减函数,
在(0,1]为减函数,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() ;
;
方法三:
![]() ,
,
当![]() 时,
时,![]() 在[0,1)上为增函数,此时
在[0,1)上为增函数,此时![]() ,故此时
,故此时![]()
当![]() 时,
时,![]() 在[0,1)上为减函数,此时
在[0,1)上为减函数,此时![]() ,故此时
,故此时![]() ,
,
综上![]() 时,
时,![]() ,
,![]() 时
时![]() .
.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
【题目】“有黑扫黑、无黑除恶、无恶治乱”,维护社会稳定和和平发展.扫黑除恶期间,大量违法分子主动投案,某市公安机关对某月连续7天主动投案的人员进行了统计,![]() 表示第
表示第![]() 天主动投案的人数,得到统计表格如下:
天主动投案的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 5 | 5 | 6 | 7 |
(1)若![]() 与
与![]() 具有线性相关关系,请根据上表提供的数据,用最小二乘法求出
具有线性相关关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)判定变量![]() 与
与![]() 之间是正相关还是负相关.(写出正确答案,不用说明理由)
之间是正相关还是负相关.(写出正确答案,不用说明理由)
(3)预测第八天的主动投案的人数(按四舍五入取到整数).
参考公式: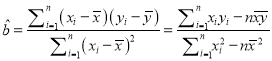 ,
, ![]() .
.