题目内容
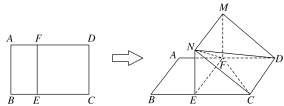
【题目】如图,多面体![]() ,
, ![]() ,
,![]()
![]() ,且
,且![]() 两两垂直.给出下列四个命题:
两两垂直.给出下列四个命题:

①三棱锥![]() 的体积为定值;
的体积为定值;
②经过![]() 四点的球的直径为
四点的球的直径为![]() ;
;
③直线![]() ∥平面
∥平面![]() ;
;
④直线![]() 所成的角为
所成的角为![]() ;
;
其中真命题的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
由题意,只要构造长方体,设OA=x,OB=y,OC=z,则x2+y2=2,x2+z2=4,y2+z2=4,解得,x=1,y=1,z=![]() ,运用棱锥的体积公式,即可判断①;运用异面直线所成角的定义,即可判断②;球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,即可判断③;由于OB∥AE,AE和平面ACD相交,即可判断④.
,运用棱锥的体积公式,即可判断①;运用异面直线所成角的定义,即可判断②;球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,即可判断③;由于OB∥AE,AE和平面ACD相交,即可判断④.
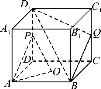
由题意,构造长方体,如右图,设OA=x,OB=y,OC=z,
则x2+y2=2,x2+z2=4,y2+z2=4,解得,x=y=1,z=![]() ,
,
对于①,三棱锥O﹣ABC的体积为![]() OC×
OC×![]() OA×OB=
OA×OB=![]() ,故①对;
,故①对;
对于②,球面经过点A、B、C、D两点的球的直径即为长方体的对角线长,
即为![]() ,故②对;
,故②对;
对于③,由于OB∥AE,AE和平面ACD相交,则OB和平面ACD相交,故③错.
对于④,由于OB∥AE,则∠DAE即为直线AD与OB所成的角,
由tan∠DAE=![]() ,则∠DAE=60°,故④对;
,则∠DAE=60°,故④对;
故选:C

练习册系列答案
相关题目